题目内容
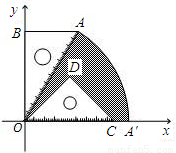
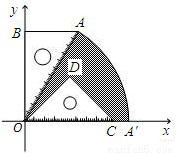
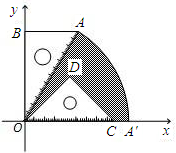
 已知:如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,AB=
已知:如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,AB=| 3 |
分析:图中阴影部分的面积等于扇形的面积减去等腰直角三角形的面积.
解答:解:在Rt△OAB中,
∵AB=
,∠AOB=30°,
∴OB=OC=3,OA=2
,
∵△OPC为等腰直角三角形,
∴OD=DC=
,
S阴影部分=S扇形OAA′-S△ODC
=
-
×
×
=2π-
,
故答案为:2π-
.
∵AB=
| 3 |
∴OB=OC=3,OA=2
| 3 |
∵△OPC为等腰直角三角形,
∴OD=DC=
| 3 |
| 2 |
| 2 |
S阴影部分=S扇形OAA′-S△ODC
=
60π×(2
| ||
| 360 |
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
=2π-
| 9 |
| 4 |
故答案为:2π-
| 9 |
| 4 |
点评:本题考查了扇形的面积计算方法,在求阴影部分的面积时,常常是几个规则图形面积的和或差.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
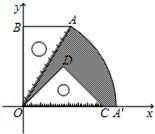
 已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.
已知:如图,有一块含30°的直角三角板OAB的直角边长BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把该套三角板放置在平面直角坐标系中,且AB=3.