题目内容
【题目】5支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是 ![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为 ![]() ;p4:五支球队成绩并列第一名的概率为
;p4:五支球队成绩并列第一名的概率为 ![]() .其中真命题是( )
.其中真命题是( )
A.p1 , p2 , p3
B.p1 , p2 , p4
C.p1 , p3 , p4
D.p2 , p3 , p4
【答案】A
【解析】解:p1为真:因为若出现四支球队并列第一名, 则第一名的胜场数不可能为3或者4(因为如此需要超过10个单场胜利者)并列赢两场,
那么自然就是五队同名次,所以不可能恰有四支球队并列第一.有可能出现恰有两支球队并列第一名,p2为真.
p3为真:5支球队单循环一共是10场比赛,
所以有210个不同的结果,由于胜率都是 ![]() ,
,
故认为所有不同比赛结果都是等可能的.记有全胜的比赛可能结果为 ![]() 种,
种,
有全败的比赛可能结果为 ![]() 种.既有全胜又有全败的结果为
种.既有全胜又有全败的结果为 ![]() 种,
种,
则既无全胜又无全败的结果为 ![]() 种.
种.
命题p3的概率为 ![]()
= ![]() ,故p3是正确的.
,故p3是正确的.
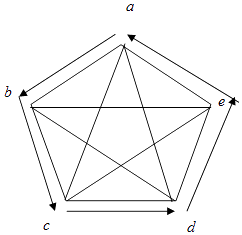
p4为假:若五支球队成绩并列第一名则必出现a>b>c>d>e>a,
同时a>c>e>b>d>a,
也就是彼得森图.规定外圈顺时针为胜,
那么外圈一共有 ![]() 种不同排列,内圈只有两种,
种不同排列,内圈只有两种,
故一共有48种,所以概率为 ![]() .
.
故选:A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目