题目内容
【题目】如图,在△ABC中,∠BAC=45°,以AB为直径的圆分别交BC,AC于D,E两点,AD交BE于F点,现给出下列命题:①![]() DE+BD=AD;②△ABE与△ABD的面积差为
DE+BD=AD;②△ABE与△ABD的面积差为![]() ED2 , 则( )
ED2 , 则( )

A.①是假命题,②是真命题 B.①是真命题,②是假命题
C.①是假命题,②是假命题 D.①是真命题,②是真命题
【答案】D
【解析】
①过点E作⊥HE交AD于H,构造等腰直角三角形,根据圆周角定理,得到角相等,证明△AEH≌△BDE,得到AH=BD,由DH=![]() DE,由等量代换得到
DE,由等量代换得到![]() DE+BD=AD;
DE+BD=AD;
②由①证得:![]() DE+BD=AD,两边平方得:2DE2=(AD-BD)2=AD2+BD2-2ADBD=AB2-2ADBD,等式的两边乘以
DE+BD=AD,两边平方得:2DE2=(AD-BD)2=AD2+BD2-2ADBD=AB2-2ADBD,等式的两边乘以![]() 得:
得:![]() DE2=
DE2=![]() AB2-
AB2-![]() ADBD=S△ABE-S△ABD,得到②是真命题.
ADBD=S△ABE-S△ABD,得到②是真命题.
①过点E作⊥HE交AD于H,
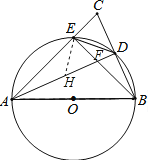
∵AB为⊙O的直径,
∴∠AEB=90°,∠ADB=90°
∵∠EAB=45°,∴∠EBA=45°,
∴∠EDA=45°,
∴∠EHD=∠EDA=45°,
∴∠AHE=∠EDB=135°,
在△AEH与△BDE中,
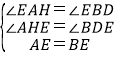 ,
,
∴△AEH≌△BDE,
∴AH=BD,
∵DH=![]() DE,
DE,
∴AD=AH+DH=BD+![]() DE,
DE,
∴①是真命题;
②∵S△ABE=![]() AEBE=
AEBE=![]() AB2,S△ABD=
AB2,S△ABD=![]() ADBD,
ADBD,
由①证得:![]() DE+BD=AD,
DE+BD=AD,
∴![]() DE=AD-BD,
DE=AD-BD,
∴2DE2=(AD-BD)2=AD2+BD2-2ADBD=AB2-2ADBD
∴![]() DE2=
DE2=![]() AB2-
AB2-![]() ADBD=S△ABE-S△ABD,
ADBD=S△ABE-S△ABD,
∴②是真命题,
故选D.

【题目】阅读可以增进人们的知识,也能陶冶人们的情操.我们要多阅读有营养的书.某校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A,B,C,D,E五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
阅读时间分组统计表
组别 | 阅读时间x(h) | 人数 |
A | 0≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | b |
D | 30≤x<40 | 140 |
E | x≥40 | c |

请结合以上信息解答下列问题:
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.