Question

已知关于x的二次函数y=x²+（2k-1）x+k²-1．
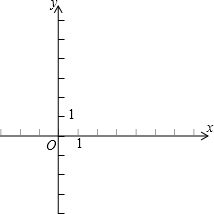
（1）若关于x的一元二次方程x²+（2k-1）x+k²-1=0的两根的平方和等于9，求k的值，并在直角坐标系（如图）中画出函数y=x²+（2k-1）x+k²-1的大致图象；
（2）在（1）的条件下，设这个二次函数的图象与x轴从左至右交于A、B两点．问函数对称轴右边的图象上，是否存在点M，使锐角△AMB的面积等于3．若存在，请求出点M的坐标；若不存在，请说明理由；
（3）在（1）、（2）条件下，若P点是二次函图象上的点，且∠PAM=90°，求△APM的面积．

Answer 1

解：（1）∵所给一元二次方程有解，
∴根的判别式△≥0，
即（2k-1）²-4（k²-1）≥0，
解得k≤；
设方程的两个根分别为x₁、x₂，
则x₁²+x₂²=9，
即（x₁+x₂）²-2x₁x₂=9，
又x₁+x₂=-（2k-1），x₁•x₂=k²-1，
分别代入上式，
解得k₁=-1或k₂=3，
∵k≤，
∴k=-1．
代入函数式中，得y=x²-3x，
配方可得y=，
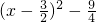即抛物线的对称轴为x=，顶点坐标为D（，-），
大致图象如下（如图）；

（2）由（1），令y=0，得x²-3x=0，
解得x₁=0，x₂=3，
∴A（0，0），B（3，0）．
这样的点存在．
其坐标为M（2，-2）．
设M（x_m，y_m），而△AMB是锐角三角形，
故＜x_m＜3，
∴y_m＜0．故有S_△AMB=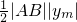==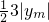3，
∴|y_m|=2，y_m=±2，舍去正值，
∴y_m=-2，
当y_m=-2时，x_m²-3x_m=-2，
解得x_m=1或x_m=2，
∵＜x_m＜3，
∴x_m=1舍去，而＜2＜3，
∴x_m=2满足条件，
∴这样的点存在，其坐标为M（2，-2）；

（3）∵M（2，-2），
∴∠MAB=45°，
∴∠BAP=45°，
∴AP所在直线的解析式为：y=x，
∵P也在抛物线上，
∴x²-3x=x，
解得：x₁=0（舍去），x₂=4，
此时y=4，
∴P（4，4），可求得线段AP长=4，线段AM长=2，
∴S_△AMP=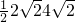=8．
分析：（1）利用根的判别式△≥0，求出k的取值范围，再利用根与系数的关系即可得出k的值，从而求出二次函数的顶点坐标与对称轴，及可得出图象；
（2）由（1），令y=0，得x²-3x=0，即可得出A（0，0），B（3，0），即可求出其坐标为M（2，-2）；
（3）由M（2，-2），得出∠BAP=45°，得出AP所在直线的解析式为：y=x，由因为P也在抛物线上，得出x²-3x=x，即可求出x的值．
点评：此题主要考查了二次函数的综合应用以及一元二次方程根的判别式与根与系数的关系等知识，此题对一元二次方程考查知识较多二次函数与一元二次方程结合是比较典型题目，同学们应注意它们之间的区别于联系．