题目内容
如图,某飞机于空中探测某座山的高度.此时飞机的飞行高度是AF=3.7千米,从飞机上观测山顶目标C的俯视角为30°.飞机继续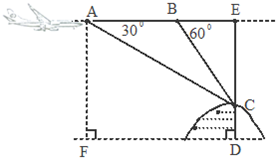 相同的高度飞行3千米到B处,此时观测目标C的俯角是60°,求此山的高度CD.(精确到0.1)
相同的高度飞行3千米到B处,此时观测目标C的俯角是60°,求此山的高度CD.(精确到0.1)
(参考数据:
≈1.414,
≈1.732)
 相同的高度飞行3千米到B处,此时观测目标C的俯角是60°,求此山的高度CD.(精确到0.1)
相同的高度飞行3千米到B处,此时观测目标C的俯角是60°,求此山的高度CD.(精确到0.1)(参考数据:
| 2 |
| 3 |
设CE=x千米.
Rt△BCE中,∠CBE=60°,
∴BE=CE÷tan60°=
x.
Rt△ACE中,∠CAE=30°,
∴AE=EC÷tan30°=
x.
∴AB=AE-BE=
x=3,
解得x=
≈2.598.
∴CD=AF-CE=AF-x=3.7-2.598≈1.1(千米).
答:此山的高度约为1.1千米.
Rt△BCE中,∠CBE=60°,
∴BE=CE÷tan60°=
| ||
| 3 |
Rt△ACE中,∠CAE=30°,
∴AE=EC÷tan30°=
| 3 |
∴AB=AE-BE=
2
| ||
| 3 |
解得x=
3
| ||
| 2 |
∴CD=AF-CE=AF-x=3.7-2.598≈1.1(千米).
答:此山的高度约为1.1千米.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目