题目内容
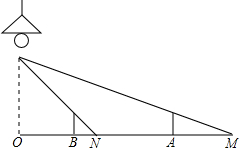
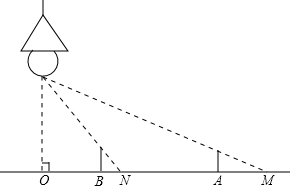 如图,路灯距地面8米,身高1.6米的小明从距离灯底(点O)20米的点A处,沿AO所在直线行走12米到达点B时,小明身影长度( )
如图,路灯距地面8米,身高1.6米的小明从距离灯底(点O)20米的点A处,沿AO所在直线行走12米到达点B时,小明身影长度( )| A、变长2.5米 | B、变短2米 | C、变短2.5米 | D、变短3米 |
分析:先根据OF⊥OM,DA⊥OM可得出△ADM∽△OFM,利用相似三角形的对应边成比例可求出AM的长,同理可求出BN的长,再求出AM与BN的差即可.
解答: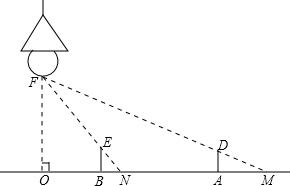 解:∵OF⊥OM,DA⊥OM,
解:∵OF⊥OM,DA⊥OM,
∴OF∥AD,
∴△ADM∽△OFM,
∴
=
,即
=
,
解得AM=5m;
同理可得,∴△BNE∽△ONF,
∴
=
即
=
,
解得BN=2m,
∴AM-BN=5-2=3m.
故选D.
 解:∵OF⊥OM,DA⊥OM,
解:∵OF⊥OM,DA⊥OM,∴OF∥AD,
∴△ADM∽△OFM,
∴
| AM |
| AM+OA |
| AD |
| OF |
| AM |
| 20+AM |
| 1.6 |
| 8 |
解得AM=5m;
同理可得,∴△BNE∽△ONF,
∴
| BN |
| OA-AB+BN |
| AD |
| OF |
即
| BN |
| 20-12+BN |
| 1.6 |
| 8 |
解得BN=2m,
∴AM-BN=5-2=3m.
故选D.
点评:本题考查的是相似三角形在实际生活中的应用,根据题意得出相似三角形,再利用相似三角形的对应边成比例求解是解答此题的关键.

练习册系列答案
相关题目
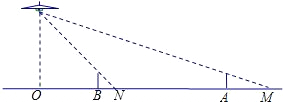 如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )| A、增大1.5米 | B、减小1.5米 | C、增大3.5米 | D、减小3.5米 |
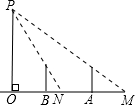 如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影长度在A处为
如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影长度在A处为
 如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时.求:
如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时.求: