题目内容
26、已知：等边△ABC中，当点D在BC边上，点E在AC边上，且BD=CE，连接AD、BE，交于点F，如图（1）易证：∠AFE=∠ABD．当点D在BC的延长线上，点E在CA的延长线上；当点D在CB的延长线上，点E在AC的延长线上．而其它条件不变时，∠AFE与∠ABD又有怎样的数量关系？请写出你的猜想，并选出一种情况加以证明？
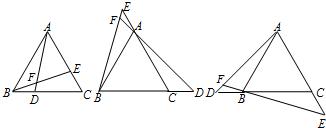
分析：根据等边三角形的三个角都等于60°，三条边都相等证明△ECB与△DBA全等，所以∠EBC=∠DAB，再根据三角形内角和等于180°求出∠AFE=120°，而∠ABD=60°，所以∠AFE=2∠ABD．
解答：解：第一种情况：∠AFE=2∠ABD．
第二种情况：2∠AFE=∠ABD．
第一种情况：
证明：在等边三角形ABC中，AB=BC，
∠BAC=∠ABC=∠ACB=60°，BD=CE，
∴△ECB≌△DBA，
∴∠EBC=∠DAB，
而△ABD中，∠DAB+∠D=180°-∠ABC=120°，
∴∠AFE=∠EBC+∠D=120°，
∴∠AFE=2∠ABD．
第二种情况：2∠AFE=∠ABD．
第一种情况：
证明：在等边三角形ABC中，AB=BC，
∠BAC=∠ABC=∠ACB=60°，BD=CE，
∴△ECB≌△DBA，
∴∠EBC=∠DAB，
而△ABD中，∠DAB+∠D=180°-∠ABC=120°，
∴∠AFE=∠EBC+∠D=120°，
∴∠AFE=2∠ABD．
点评：本题主要考查等边三角形的性质和全等三角形的判与性质；仔细分析图形特点并熟练掌握性质和定理，题目便不难解决，分情况讨论是正确解答本题的关键．
练习册系列答案
相关题目
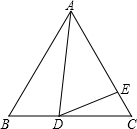已知：等边△ABC中，AB、cosB是关于x的方程x2-4mx-
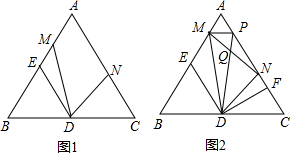连DM，作DN平分∠MDC交AC于N．
