题目内容
【题目】如图,某农场有一块长40m,宽32m的矩形种植地,为方便管理,准备沿平行于两边的方向纵、横各修建一条等宽的小路,要使种植面积为1140m2,求小路的宽.设小路的宽为x,则可列方程为( )

A. (40-2x)(32-x)=1140 B. (40-x)(32-x)=1140
C. (40-x)(32-2x)=1140 D. (40-2x)(32-2x)=1140
【答案】B
【解析】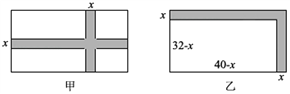
如图甲所示,种植面积应为图甲中白色区域的总面积. 利用平移的方法将两条小路平移至地块的边上,将图甲中白色区域的面积合并成如图乙所示的白色矩形区域的面积进行计算.
由题意,得
图乙中白色矩形区域的面积可表示为:(40-x)(32-x),
由于已知种植面积为1140m2,故可列方程:
(40-x)(32-x)=1140.
故本题应选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
