题目内容
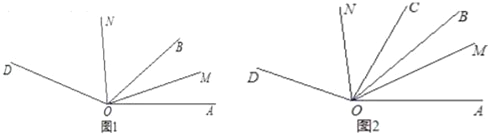
【题目】已知:∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线,
(1)如图1,若OM平分∠AOB,ON平分∠DOB,当OB绕点O在∠AOD内旋转时,求∠MON的大小.
(2)如图2.若∠BOC=20°,OM平分∠AOC,ON平分∠DOB,当∠COB绕点O在∠AOD内旋转时,求∠MON的大小.
【答案】(1)80°;(2)70°
【解析】(1)根据角平分线的定义求出∠BOM和∠BON,然后根据∠MON=∠BOM+∠BON代入数据进行计算即可得解;
(2)设∠AOB=x,表示出∠BOD=α-x,根据角平分线的定义表示出∠COM和∠BON,然后根据∠MON=∠COM+∠BON-∠BOC列式计算即可得解.
(1)∵∠AOD=160°,OM平分∠AOB,ON平分∠BOD
∴∠MOB=![]() ∠AOB,∠BON=
∠AOB,∠BON=![]() ∠BOD
∠BOD
即∠MON=∠MOB+∠BON=![]() ∠AOB+
∠AOB+![]() ∠BOD=
∠BOD=![]() (∠AOB+∠BOD)
(∠AOB+∠BOD)
=![]() ∠AOD=80°;
∠AOD=80°;
(2)∵OM平分∠AOC,ON平分∠BOD
∴∠MOC=![]() ∠AOC,∠BON=
∠AOC,∠BON=![]() ∠BOD
∠BOD
即∠MON=∠MOC+∠BON﹣∠BOC=![]() ∠AOC+
∠AOC+![]() ∠BOD﹣∠BOC
∠BOD﹣∠BOC
=![]() (∠AOC+∠BOD)﹣∠BOC=
(∠AOC+∠BOD)﹣∠BOC=![]() ×180°﹣20°
×180°﹣20°
=70°
“点睛”本题考查了角的计算,角平分线的定义,准确识图是解题的关键,难点在于要注意整体思想的利用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目