题目内容
【题目】观察并探求下列各问题：
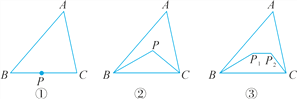
(1)如图①，在△ABC中，P为边BC上一点，则BP＋PC__ __AB＋AC(填“＞”“＜”或“＝”)．
(2)将(1)中的点P移到△ABC内，得图②，试观察比较△BPC的周长与△ABC的周长的大小，并说明理由．
(3)将(2)中的点P变为两个点P1，P2，得图③，试观察比较四边形BP1P2C的周长与△ABC的周长的大小，并说明理由．
【答案】（1）＜；（2）＜；（3）＜.
【解析】试题分析：（1）根据三角形中两边之和大于第三边，即可得出结果，
（2）可延长BP交AC与M，根据两边之和大于第三边，即可得出结果，
（3）分别延长BP1、CP2交于M，再根据（2）中得出的BM+CM＜AB+AC，可得出BP1+P1P2+P2C＜BM+CM＜AB+AC，即可得出结果．
试题解析：（1）BP+PC＜AB+AC，理由：三角形两边之和大于第三边，
（2）△BPC的周长＜△ABC的周长．理由：
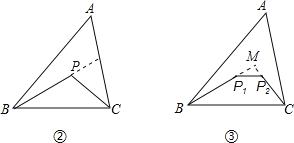
如图，延长BP交AC于M，在△ABM中，BP+PM＜AB+AM，在△PMC中，PC＜PM+MC，两式相加得BP+PC＜AB+AC，于是得：△BPC的周长＜△ABC的周长，
（3）四边形BP1P2C的周长＜△ABC的周长，理由：
如图，分别延长BP1、CP2交于M，由（2）知，BM+CM＜AB+AC，又P1P2＜P1M+P2M，
可得，BP1+P1P2+P2C＜BM+CM＜AB+AC，可得结论.
练习册系列答案
相关题目
