题目内容
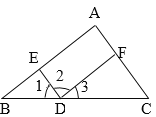
【题目】如图①,先把一矩形![]() 纸片上下对折,设折痕为
纸片上下对折,设折痕为![]() ;如图②,再把
;如图②,再把
点![]() 叠在折痕线
叠在折痕线![]() 上,得到
上,得到![]()
![]() .过
.过![]() 点作
点作![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
(1)求证: ![]() ∽
∽![]() ;
;
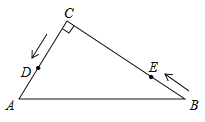
(2)在图②中,如果沿直线![]() 再次折叠纸片,点
再次折叠纸片,点![]() 能否叠在直线
能否叠在直线![]() 上?请说明理由;
上?请说明理由;
(3)在(2)的条件下,若![]() ,求
,求![]() 的长度.
的长度.

【答案】(1)(2)见解析;(3)![]()
【解析】试题分析:(1)由题意可以得到∠BPE=∠AQB=90°,通过角的转化可以得到∠BEP=∠ABQ,从而可以得到△PBE∽△QAB;
(2)根据折叠的知识可以得到QB=PB,由第(1)问中的相似可以得到对应边成比例,通过转化可以得到△PBE∽△BAE,从而可以解答本题;
(3)由题意和第(2)问可以得到∠AEB=∠BEP=60°,∠ABE=90°,又因为AB=![]() ,sin∠AEB=
,sin∠AEB=![]() ,从而可以得到AE的长度.
,从而可以得到AE的长度.
试题解析:(1)证明:∵PQ⊥MN,BN∥EC∥AD,∴∠BPE=∠AQB=∠PBN=∠NBQ=90°,∴∠PBE+∠BEP=90°,又∵∠PBE+∠ABQ=180°﹣∠ABE=180°﹣90°=90°,∴∠BEP=∠ABQ,在△PBE和△QAB中,∵∠BPE=∠AQB,∠BEP=∠ABQ,∴△PBE∽△QAB;
(2)点A能叠在直线EC上,理由:∵△PBE∽△QAB,∴ ![]() ,∵由折叠可知,QB=PB,∴
,∵由折叠可知,QB=PB,∴![]() ,即
,即![]() ,又∵∠ABE=∠BPE=90°,∴△PBE∽△BAE,∴∠AEB=∠PEB,∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
,又∵∠ABE=∠BPE=90°,∴△PBE∽△BAE,∴∠AEB=∠PEB,∴沿直线EB再次折叠纸片,点A能叠在直线EC上;
(3)解:由(2)可知,∠AEB=∠PEB,而由折叠过程知:2∠AEB+∠PEB=180°,∴∠AEB=∠PEB=60°,在Rt△ABE中,sin∠AEB=![]() ,∴AE=
,∴AE= .
.

【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.
白纸张数x(张) | 1 | 2 | 3 | 4 | 5 | … |
纸条总长度y(cm) | 20 | 54 | 71 | … |
(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
【题目】为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时) | 0 | 1 | 2 | 3 | … |
油箱剩余油量 Q(升) | 100 | 94 | 88 | 82 | … |
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).