Question

如图，平面直角坐标系中，矩形OABC的对角线AC=12，tan∠ACO=，

（1）求B、C两点的坐标；
（2）把矩形沿直线DE对折使点C落在点A处，DE与AC相交于点F，求直线DE的解析式；
（3）若点M在直线DE上，平面内是否存在点N，使以O、F、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．

Answer 1

（1）C的坐标是：（6，0），B的坐标是（6，6）。
（2）直线DE的解析式是：y=x﹣6。
（3）N的坐标是：（3，）或（﹣3，）或（，3）。

试题分析：（1）根据三角函数求得OA以及OC的长度，则C、B的坐标即可得到。
解：在直角△OAC中，，
∴设OA=x，则OC=3x，
根据勾股定理得：（3x）²+（x）²=AC²，即9x²+3x²=144，解得：x=2。
∴C的坐标是：（6，0），B的坐标是（6，6）。
（2）直线DE是AC的中垂线，应用待定系数法以及锐角三角函数定义即可求得DE的解析式。
解：∵F是AC的中点，∴根据对折的性质，F的坐标是（3，3）。
设D（d，0），则根据对折的性质，E（，6）。
如图，过点E作EH⊥OC于点H，则HE=6，DH=。

易证∠DEH=∠ACO，
∵，∴，
即，解得。
∴D（，0）
设直线DE的解析式是y=" k" x+b，将点D、F的坐标代入，得
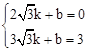，解得
∴直线DE的解析式是：y=x﹣6。
（3）分当FM是菱形的边和当OF是对角线两种情况进行讨论，利用三角函数即可求得N的坐标：
OF=AC=6。
∵，
∴30°。∴DE与x轴夹角是60°。
当FM是菱形的边时（如图），ON∥FM，

则∠NOC=60°或120°。
当∠NOC=60°时，过N作NG⊥y轴，
∴NG=ON•sin30°=6×=3，OG=ON•cos30°=6×=。
∴N的坐标是（3，）。
当∠NOC=120°时，与当∠NOC=60°时关于原点对称，则N的坐标是（﹣3，）。
当OF是对角线时（如图），MN关于OF对称。

∵F的坐标是（，3），∴∠FOD=∠NOF=30°。
在Rt△ONH中，OH=OF=3，。
作NL⊥y轴于点L，
在Rt△ONL中，∠NOL=30°，
∴NL=ON=，OL=ON•cos30°=2×=3。
∴N的坐标是（，3）。
综上所述，N的坐标是：（3，）或（﹣3，）或（，3）。