题目内容
试证明:关于x的方程(x-1)(x+2m)=m2,总有两个不相等的实数根.
分析:先把方程化为一般式得到x2+(2m-1)x-m2-2m=0,再计算判别式得△=8m2+4m+1,配方后得到△=8(m+
)2+
,然后根据非负数的性质得到△>0,再根据判别式的意义即可得到结论.
| 1 |
| 4 |
| 1 |
| 2 |
解答:证明:x2+(2m-1)x-m2-2m=0,
△=(2m-1)2-4×1×(-m2-2m)
=8m2+4m+1,
=8(m+
)2+
,
∵8(m+
)2≥0,
∴8(m+
)2+
>0,即△>0,
∴方程总有两个不相等的实数根.
△=(2m-1)2-4×1×(-m2-2m)
=8m2+4m+1,
=8(m+
| 1 |
| 4 |
| 1 |
| 2 |
∵8(m+
| 1 |
| 4 |
∴8(m+
| 1 |
| 4 |
| 1 |
| 2 |
∴方程总有两个不相等的实数根.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 的解为x1=3,
的解为x1=3,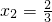 ;
; 的解为x1=4,
的解为x1=4, ;
; 的解为x1=5,
的解为x1=5, .
. 的解是______;
的解是______; .
. 的解为x1=3,
的解为x1=3, ;
; 的解为x1=4,
的解为x1=4, ;
; 的解为x1=5,
的解为x1=5, .
. 的解是_________;
的解是_________; 的解的方法,证明你的猜想;
的解的方法,证明你的猜想;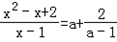 .
.