题目内容
阅读下面材料,并完成下列问题.不难求得方程x+
| 2 |
| x |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| x |
| 2 |
| 4 |
| 2 |
| 4 |
| 2 |
| x |
| 2 |
| 5 |
| 2 |
| 5 |
(1)观察上述方程及其解,可猜想关于x的方程x+
| 2 |
| x |
| 2 |
| a |
(2)试求出关于x的方程x+
| 2 |
| x |
| 2 |
| a |
(3)利用你猜想的结论,解关于x的方程
| x2-x+2 |
| x-1 |
| 2 |
| a-1 |
分析:(1)根据规律可直接得出关于x的方程x+
=a+
的解即可;
(2)去分母,转化成整式方程求解即可;
(3)先化简,得出上面的形式,再求解即可.
| 2 |
| x |
| 2 |
| a |
(2)去分母,转化成整式方程求解即可;
(3)先化简,得出上面的形式,再求解即可.
解答:解:(1)猜想:x的方程x+
=a+
的解是x1=a,x2=
.
(2)去分母,得到ax2+2a=a2x+2x,
∴ax(x-a)+2(a-x)=0,
∴(x-a)(ax-2)=0,
x1=a,x2=
.
(3)解方程(x2-x+2)÷(x-1)=a+
[x(x-1)+2]÷(x-1)=a+
x+
=a+
两边同加-1,(x-1)+
=(a-1)+
所以x-1=a-1,或者x-1=
因此 x1=a,x2=1+
=
.
| 2 |
| x |
| 2 |
| a |
| 2 |
| a |
(2)去分母,得到ax2+2a=a2x+2x,
∴ax(x-a)+2(a-x)=0,
∴(x-a)(ax-2)=0,
x1=a,x2=
| 2 |
| a |
(3)解方程(x2-x+2)÷(x-1)=a+
| 2 |
| a-1 |
[x(x-1)+2]÷(x-1)=a+
| 2 |
| a-1 |
x+
| 2 |
| x-1 |
| 2 |
| a-1 |
两边同加-1,(x-1)+
| 2 |
| x-1 |
| 2 |
| a-1 |
所以x-1=a-1,或者x-1=
| 2 |
| a-1 |
| 2 |
| a-1 |
| a+1 |
| a-1 |
点评:本题是一个找规律的题目,考查了解分式方程,是基础知识要熟练掌握.

练习册系列答案
相关题目
 的解为x1=3,
的解为x1=3,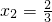 ;
; 的解为x1=4,
的解为x1=4, ;
; 的解为x1=5,
的解为x1=5, .
. 的解是______;
的解是______; .
. 的解为x1=3,
的解为x1=3, ;
; 的解为x1=4,
的解为x1=4, ;
; 的解为x1=5,
的解为x1=5, .
. 的解是_________;
的解是_________; 的解的方法,证明你的猜想;
的解的方法,证明你的猜想;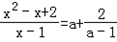 .
. 的解为x1=3,
的解为x1=3, ;
; 的解为x1=4,
的解为x1=4, ;
; 的解为x1=5,
的解为x1=5, .
. 的解是______;
的解是______; 的解的方法证明你的猜想;
的解的方法证明你的猜想; .
.