题目内容
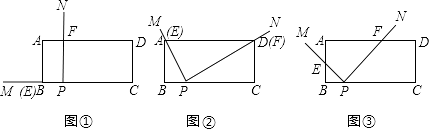
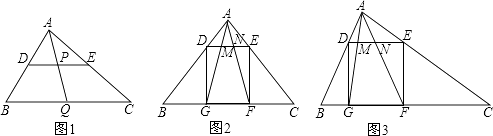
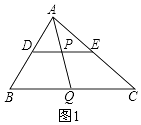
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整. 原题:如图1,在△ABC中,点D、E、Q分别在AB、AC、BC上,且DE∥BC,AQ交DE于点P,求证: ![]() .
.
(1)尝试探究:在图1中,由DP∥BQ得△ADP△ABQ(填“≌”或“∽”),则 ![]() = , 同理可得
= , 同理可得 ![]() =
= ![]() ,从而
,从而 ![]() .
.
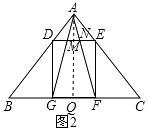
(2)类比延伸:如图2,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交DE于M、N两点,若AB=AC=1,则MN的长为 .
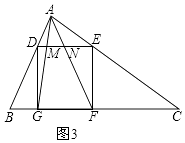
(3)拓展迁移:如图3,在△ABC中,∠BAC=90°,正方形DEFG的四个顶点在△ABC的边上,连接AG、AF分别交于DE于M、N两点,AB<AC,求证:MN2=DMEN.
【答案】
(1)S;![]()
(2)![]()
(3)解:证明:如图3,∵∠B+∠C=90°∠CEF+∠C=90°,
∴∠B=∠CEF,
又∵∠BGD=∠EFC,
∴△BGD∽△EFC,
∴ ![]() ,
,
∴DGEF=CFBG,
又∵DG=GF=EF,
∴GF2=CFBG,
由(1)得 ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() ×
× ![]() =
= ![]() ×
× ![]() ,
,
∴( ![]() )2=
)2= ![]() ×
× ![]() ,
,
∵GF2=CFBG,
∴MN2=DMEN.
【解析】(1)解:如图1,∵DP∥BQ, ∴△ADP∽△ABQ,
∴ ![]() =
= ![]() ,
,
同理可得△ACQ∽△APE,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.
所以答案是:∽, ![]()
2)解:如图2所示,作AQ⊥BC于点Q.
∵BC边上的高AQ= ![]() ,
,
∵DE=DG=GF=EF=BG=CF,
∴DE:BC=1:3,
又∵DE∥BC,
∴AD:AB=1:3,
∴AD= ![]() ,DE=
,DE= ![]() ,
,
∵DE边上的高为 ![]() ,MN:GF=
,MN:GF= ![]() :
: ![]() ,
,
∴MN: ![]() =
= ![]() :
: ![]() ,
,
∴MN= ![]() .
.
所以答案是: ![]()
【考点精析】通过灵活运用相似三角形的判定与性质,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案