Question

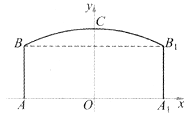
如图，隧道的截面由抛物线AED和矩形ABCD构成，矩形的长BC为8m，宽AB为2m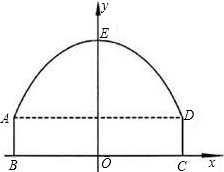，以BC所在的直线为x轴，线段BC的中垂线为y轴，建立平面直角坐标系．y轴是抛物线的对称轴，顶点E到坐标原点O的距离为6m．
（1）求抛物线的解析式；
（2）如果该隧道内设双行道，现有一辆货运卡车高4.2m，宽2.4米，这辆货运卡车能否通过该隧道？通过计算说明你的结论．

Answer 1

解：（1）设抛物线的解析式为y=ax²+bx+c，由对称轴是y轴得b=0，
由EO=6，得c=6，
又∵抛物线经过点D（4，2），
所以：16a+4b+6=2，
解得a=
所求抛物线的解析式为：y=x²+6．

（2）取x=±2.4，代入（1）所求得的解析式中，
求得y=4.56＞4.2
故这辆货运卡车能通过隧道．
分析：（1）根据抛物线在坐标系中的特殊位置，可以设抛物线的一般式，顶点式，求抛物线的解析式．
（2）抛物线的实际应用问题中，可以取自变量的值，求函数值．
点评：求抛物线解析式有几种方法，因题而异，灵活处理．会找抛物线上几个关键点的坐标，确定抛物线解析式．