题目内容
 如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论中:①∠BAD=∠CAD;②AD上任意一点到AB、AC的距离相等;③BD=CD;④若点P在直线AD上,则PB=PC.其中正确的是
如图,△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,下列结论中:①∠BAD=∠CAD;②AD上任意一点到AB、AC的距离相等;③BD=CD;④若点P在直线AD上,则PB=PC.其中正确的是
- A.①
- B.①②
- C.①②③
- D.①②③④
D
分析:由题意知,△ABC是等腰三角形,由三线合一的性质知,高AD也是顶角的平分线,也是底边BC的中线,则①③正确;再由角平分线的性质得出②正确;由AD是BC的中垂线,根据线段中垂线的性质得出④正确,故可得到4个说法均正确.
解答: 解:∵AB=AC,
解:∵AB=AC,
∴△ABC是等腰三角形,
又∵AD⊥BC于D,
∴∠BAD=∠CAD,BD=CD,故①③正确;
∵∠BAD=∠CAD,
∴AD上任意一点到AB、AC的距离相等,故②正确;
∵AD是BC的中垂线,
∴若点P在直线AD上,则PB=PC,故④正确.
故选D.
点评:本题考查了等腰三角形“三线合一”的性质,角平分线的性质及线段中垂线的性质,比较简单.
等腰三角形“三线合一”的性质:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
角平分线的性质:角的平分线上的点到角的两边的距离相等.
线段中垂线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等.
分析:由题意知,△ABC是等腰三角形,由三线合一的性质知,高AD也是顶角的平分线,也是底边BC的中线,则①③正确;再由角平分线的性质得出②正确;由AD是BC的中垂线,根据线段中垂线的性质得出④正确,故可得到4个说法均正确.
解答:
 解:∵AB=AC,
解:∵AB=AC,∴△ABC是等腰三角形,
又∵AD⊥BC于D,
∴∠BAD=∠CAD,BD=CD,故①③正确;
∵∠BAD=∠CAD,
∴AD上任意一点到AB、AC的距离相等,故②正确;
∵AD是BC的中垂线,
∴若点P在直线AD上,则PB=PC,故④正确.
故选D.
点评:本题考查了等腰三角形“三线合一”的性质,角平分线的性质及线段中垂线的性质,比较简单.
等腰三角形“三线合一”的性质:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
角平分线的性质:角的平分线上的点到角的两边的距离相等.
线段中垂线的性质:线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
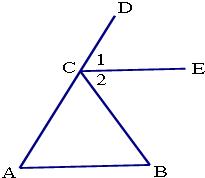 26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.
26、已知:如图,△ABC中,点D在AC的延长线上,CE是∠DCB的角平分线,且CE∥AB.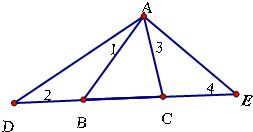 27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE.
27、已知:如图,△ABC中,∠BAC=60°,D、E两点在直线BC上,连接AD、AE. 27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M
27、如图,△ABC中,AD⊥BC于D,DN⊥AC于N,DM⊥AB于M 14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )
14、如图,△ABC中,∠BAC=120°,AD⊥BC于D,且AB+BD=DC,则∠C的大小是( )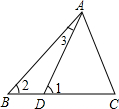 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.