题目内容
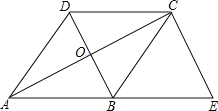
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若AB=5, BD=6时,求△ACE的周长.
【答案】(1)见详解;(2)24
【解析】
(1)根据菱形的性质,可得AB=CD,AB∥CD,然后证明四边形BECD是平行四边形,即可得到结论成立;
(2)易得AE=10,CE=BD=6,由OB是中位线,得到OB∥CE,则CE⊥AC,利用勾股定理求出AC=8,即可求出周长.
(1)证明:四边形ABCD是菱形,
∴AB=CD,AB∥CD,
又∵BE=AB,
∴BE=CD,BE∥CD,
∴四边形BECD 是平行四边形,
∴BD=EC;
(2)解:∵BE=AB=5,
∴AE=10,CE=BD=6,
在菱形ABCD中,BD⊥AC,
∵点O是AC中点,点B是AE中点,
∴OB∥CE,
∴CE⊥AC,
在Rt△ACE中,由勾股定理,得
![]() ,
,
∴△ACE的周长为:![]() .
.

练习册系列答案
相关题目