题目内容
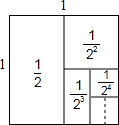 在数学兴趣小组活动中,小明为了求
在数学兴趣小组活动中,小明为了求| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
分析:根据图中可知正方形的面积依次为
,
,…
.根据组合图形的面积计算可得.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
解答:解:
+
+
+
+…+
=1-
.
答:
+
+
+
+…+
的值为1-
.
故答案为:1-
.
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| 1 |
| 2n |
答:
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 24 |
| 1 |
| 2n |
| 1 |
| 2n |
故答案为:1-
| 1 |
| 2n |
点评:考查了正方形的面积公式,及组合图形的面积计算.正方形的面积为1,根据图中二等分n次,面积为
.
| 1 |
| 2n |

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
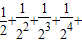 …+
…+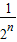 的值,在边长为1的正方形中,设计了如图所示的几何图形.则
的值,在边长为1的正方形中,设计了如图所示的几何图形.则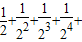 …+
…+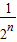 的值为 (结果用n表示).
的值为 (结果用n表示).