题目内容
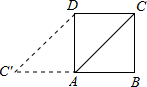如图，已知正方形ABCD的边长为3，如果将线段AC绕点A旋转后，点C落在BA的延长线上的C′点处，那么sin∠ADC′=
| ||
| 3 |
| ||
| 3 |
分析：根据题意知AB=3，由勾股定理、旋转的性质知AC'=AC=
；然后在直角三角形AC′D中根据勾股定理可求得DC'，然后根据锐角三角函数的定义即可求得sin∠ADC′的值．
| 2 |
解答：解：∵正方形ABCD的边长为3，
∴AD=AB=3，AC=3
；
∵线段AC绕点A旋转后，点C落在BA的延长线上的C′点处，
∴AC=AC′=3
；
在直角三角形ADC′中，DC′=
=3
；
∴sin∠ADC′=
=
=
；
故答案是：
．
解：∵正方形ABCD的边长为3，∴AD=AB=3，AC=3
| 2 |
∵线段AC绕点A旋转后，点C落在BA的延长线上的C′点处，
∴AC=AC′=3
| 2 |
在直角三角形ADC′中，DC′=
| AD2+AC′2 |
| 3 |
∴sin∠ADC′=
| AC′ |
| C′D |
3
| ||
3
|
| ||
| 3 |
故答案是：
| ||
| 3 |
点评：本题综合考查了旋转的性质、正方形的性质以及锐角三角函数的定义．解题时，要挖掘隐含在题中的已知条件“AC=AC′”．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
如图，已知正方形ABCD的边AB与正方形AEFM的边AM在同一直线上，直线BE与DM交于点N．求证：BN⊥DM．
（2013•北碚区模拟）如图，已知正方形ABCD，点E是BC上一点，点F是CD延长线上一点，连接EF，若BE=DF，点P是EF的中点．
如图，已知正方形ABCD，点E在BC边上，将△DCE绕某点G旋转得到△CBF，点F恰好在AB边上．
如图，已知正方形ABCD的对角线交于O，过O点作OE⊥OF，分别交AB、BC于E、F，若AE=4，CF=3，则EF的值是（ ）
如图，已知正方形ABCD的对角线AC，BD相交于点O，E是AC上的一点，过点A作AG⊥BE，垂足为G，AG交BD于点F．