题目内容
 如图,在△BEF中,∠BEF=90°,BE=EF,四边形ABCD是正方形,连接DF,G为DF的中点,连接EG、CG.证明:EG=CG,EG⊥CG.
如图,在△BEF中,∠BEF=90°,BE=EF,四边形ABCD是正方形,连接DF,G为DF的中点,连接EG、CG.证明:EG=CG,EG⊥CG.
证明: 取BF中点H,连接EH,GH,连接BD,取BD中点O,连接OG,OC,
取BF中点H,连接EH,GH,连接BD,取BD中点O,连接OG,OC,
∵CB=CD,∠DCB=90°,
∴CO= BD,
BD,
∵DG=GF,
∴GH∥BD,GH= BD,
BD,
∴OG∥BF,OG= BF,
BF,
∴OC=GH,
∵△BEF是等腰直角三角形,
∴EH= BF,
BF,
∴EH=OG,
∴四边形OBHG是平行四边形,
∴∠BOG=∠BHG,
∵∠BOC=∠BHE=90°,
∴∠GOC=∠EHG,
在△GOC和△EHG中
∵ ,
,
∴△GOC≌△EHG(SAS),
∴EG=CG,∠EGH=∠GCO,
∴∠EGC=∠EGH+∠HGO+∠CGO,
=∠CGO+∠GCO+∠GOD,
=180°-∠DOC,
=180°-90°,
=90°,
∴EG⊥CE,即EG=CG.EG⊥CG.
分析:取BF中点H,连接EH,GH,连接BD,取BD中点O,连接OG,OC,根据等腰直角三角形性质求出CO= BD,CO⊥BD,根据三角形的中位线得出GH∥BD,GH=
BD,CO⊥BD,根据三角形的中位线得出GH∥BD,GH= BD,OG∥BF,OG=
BD,OG∥BF,OG= BF,推出OC=GH,根据等腰直角三角形性质得出EH=
BF,推出OC=GH,根据等腰直角三角形性质得出EH= BF,推出四边形OBHG是平行四边形,求出∠GOC=∠EHG,证△GOC≌△EHG,推出EG=CG,∠EGH=∠GCO,求出∠EGC的度数即可.
BF,推出四边形OBHG是平行四边形,求出∠GOC=∠EHG,证△GOC≌△EHG,推出EG=CG,∠EGH=∠GCO,求出∠EGC的度数即可.
点评:本题综合考查了平行四边形性质和判定,三角形的内角和定理,直角三角形斜边上中线,正方形性质,三角形的中位线等知识点的应用,主要考查学生的推理能力,题目综合性比较强,难度较大.
 取BF中点H,连接EH,GH,连接BD,取BD中点O,连接OG,OC,
取BF中点H,连接EH,GH,连接BD,取BD中点O,连接OG,OC,∵CB=CD,∠DCB=90°,
∴CO=
 BD,
BD,∵DG=GF,
∴GH∥BD,GH=
 BD,
BD,∴OG∥BF,OG=
 BF,
BF,∴OC=GH,
∵△BEF是等腰直角三角形,
∴EH=
 BF,
BF,∴EH=OG,
∴四边形OBHG是平行四边形,
∴∠BOG=∠BHG,
∵∠BOC=∠BHE=90°,
∴∠GOC=∠EHG,
在△GOC和△EHG中
∵
 ,
,∴△GOC≌△EHG(SAS),
∴EG=CG,∠EGH=∠GCO,
∴∠EGC=∠EGH+∠HGO+∠CGO,
=∠CGO+∠GCO+∠GOD,
=180°-∠DOC,
=180°-90°,
=90°,
∴EG⊥CE,即EG=CG.EG⊥CG.
分析:取BF中点H,连接EH,GH,连接BD,取BD中点O,连接OG,OC,根据等腰直角三角形性质求出CO=
 BD,CO⊥BD,根据三角形的中位线得出GH∥BD,GH=
BD,CO⊥BD,根据三角形的中位线得出GH∥BD,GH= BD,OG∥BF,OG=
BD,OG∥BF,OG= BF,推出OC=GH,根据等腰直角三角形性质得出EH=
BF,推出OC=GH,根据等腰直角三角形性质得出EH= BF,推出四边形OBHG是平行四边形,求出∠GOC=∠EHG,证△GOC≌△EHG,推出EG=CG,∠EGH=∠GCO,求出∠EGC的度数即可.
BF,推出四边形OBHG是平行四边形,求出∠GOC=∠EHG,证△GOC≌△EHG,推出EG=CG,∠EGH=∠GCO,求出∠EGC的度数即可.点评:本题综合考查了平行四边形性质和判定,三角形的内角和定理,直角三角形斜边上中线,正方形性质,三角形的中位线等知识点的应用,主要考查学生的推理能力,题目综合性比较强,难度较大.

练习册系列答案
相关题目
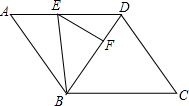 如图,在?ABCD中,CD=10,
如图,在?ABCD中,CD=10, 如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,有下列结论:
如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,有下列结论: 如图,在△BEF中,∠BEF=90°,BE=EF,四边形ABCD是正方形,连接DF,G为DF的中点,连接EG、CG.证明:EG=CG,EG⊥CG.
如图,在△BEF中,∠BEF=90°,BE=EF,四边形ABCD是正方形,连接DF,G为DF的中点,连接EG、CG.证明:EG=CG,EG⊥CG.