题目内容
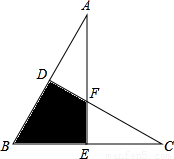
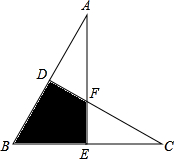 将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.
将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.
分析:根据BD=BE,利用三角函数即可求得BD的长,进而求得AD的长,则△ADF的面积即可求得,然后根据S四边形DBEF=S△ABE-S△ADF从而求解.
解答:解:在Rt△AEB中,∠B=60°,AB=10
∴BE=AB•cos60°=10×
=5
AE=AB•sin60°=10×
=5
由题意BE=BD=5,从而AD=5,在Rt△ADF中,∠A=30°,AD=5
∴DF=AD•tan30°=5×
=
∴S四边形DBEF=S△ABE-S△ADF=
×5×5
-
×5×
=
.
∴BE=AB•cos60°=10×
| 1 |
| 2 |
AE=AB•sin60°=10×
| ||
| 2 |
| 3 |
由题意BE=BD=5,从而AD=5,在Rt△ADF中,∠A=30°,AD=5
∴DF=AD•tan30°=5×
| ||
| 3 |
5
| ||
| 3 |
∴S四边形DBEF=S△ABE-S△ADF=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
5
| ||
| 3 |
25
| ||
| 3 |
点评:本题主要考查了解直角三角形,正确求得AD的长,理解解直角三角形的条件是关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
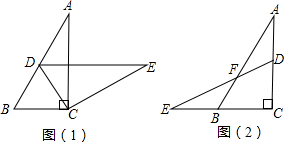
 将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.
将两块大小完全相同的直角三角板△AEB和△CDB如图摆放,斜边AB=BC=10cm,∠B=60°.求图中两块三角板重叠部分(即四边形DBEF)的面积.