题目内容
如图,某同学在数学实验课上,将两块大小完全相同的含30°角的直角三角板拼成如下两个图形.(1)在图(1)中,求∠ACD的度数;
(2)在图(2)中,求证:AF=EF.
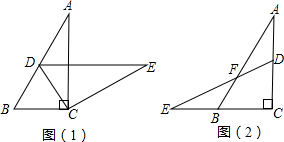
分析:(1)观察图形,AC⊥DE,先求出∠ACE的度数,然后利用∠DCE是直角即可求解;
(2)先根据直角三角形边的关系求出AD=BE,然后利用角角边定理即可证明△AFD与△EFB全等,再根据全等三角形对应边相等即可证明.
(2)先根据直角三角形边的关系求出AD=BE,然后利用角角边定理即可证明△AFD与△EFB全等,再根据全等三角形对应边相等即可证明.
解答:(1)解:观察可知,AC⊥DE,
∴∠ACE=90°-∠E=90°-30°=60°,
∴∠ACD=∠DCE-∠ACE=90°-60°=30°;
(2)证明:∵两直角三角板完全相同,
∴AC=CE,BC=CD,
∴AC-CD=CE-BC,
即AD=BE,
在△AFD与△EFB中,
,
∴△AFD≌△EFB(AAS),
∴AF=EF.
∴∠ACE=90°-∠E=90°-30°=60°,
∴∠ACD=∠DCE-∠ACE=90°-60°=30°;
(2)证明:∵两直角三角板完全相同,
∴AC=CE,BC=CD,
∴AC-CD=CE-BC,
即AD=BE,
在△AFD与△EFB中,
|
∴△AFD≌△EFB(AAS),
∴AF=EF.
点评:本题考查了全等三角形的判定与性质,熟悉直角三角板的边、角关系是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目


 22、如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图上阴影部分),但是一不小心,少画了一个,请你给他补上一个,可以组合成正方体,你有几种画法请在图上用阴影注明,并标注不同画法的序号(如:①,②…).
22、如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图上阴影部分),但是一不小心,少画了一个,请你给他补上一个,可以组合成正方体,你有几种画法请在图上用阴影注明,并标注不同画法的序号(如:①,②…).