题目内容
（2013•扬州）如图，在梯形ABCD中，AD∥BC，AB=AD=CD，BC=12，∠ABC=60°，则梯形ABCD的周长为30
30
．分析：过A作AE∥DC交BC于E，得出等边三角形ABE和平行四边形ADCE，推出AB=AD=DC=BE=CE，求出AD长，即可得出答案．
解答：解：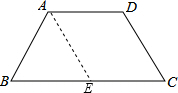
过A作AE∥DC交BC于E，
∵AD∥BC，
∴四边形ADCE是平行四边形，
∴AD=EC=DC，AE=DC，
∵AB=CD，
∴AB=AE，
∴△ABE是等边三角形，
∴BE=AB=AE=DC=AD=CE，
∵BC=12，
∴AB=AD=DC=6，
∴梯形ABCD的周长是AD+DC+BC+AB=6+6+12+6=30，
故答案为：30．
过A作AE∥DC交BC于E，
∵AD∥BC，
∴四边形ADCE是平行四边形，
∴AD=EC=DC，AE=DC，
∵AB=CD，
∴AB=AE，
∴△ABE是等边三角形，
∴BE=AB=AE=DC=AD=CE，
∵BC=12，
∴AB=AD=DC=6，
∴梯形ABCD的周长是AD+DC+BC+AB=6+6+12+6=30，
故答案为：30．
点评：本题考查了平行四边形性质和判定，等边三角形的性质和判定，等腰梯形性质的应用，解此题的关键是能把等腰梯形转化成平行四边形和等边三角形．
练习册系列答案
名校课堂系列答案
相关题目
（2013•扬州）如图，在扇形OAB中，∠AOB=110°，半径OA=18，将扇形OAB沿过点B的直线折叠，点O恰好落在
（2013•扬州）如图，已知⊙O的直径AB=6，E、F为AB的三等分点，M、N为
（2013•扬州）如图，抛物线y=x2-2x-8交y轴于点A，交x轴正半轴于点B．