题目内容
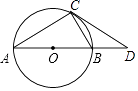
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
(1)单摆的长度( ![]() ≈1.7);
≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1).
【答案】
(1)
解:如图,过点A作AP⊥OC于点P,过点B作BQ⊥OC于点Q,

∵∠EOA=30°、∠FOB=60°,且OC⊥EF,
∴∠AOP=60°、∠BOQ=30°,
设OA=OB=x,
则在Rt△AOP中,OP=OAcos∠AOP= ![]() x,
x,
在Rt△BOQ中,OQ=OBcos∠BOQ= ![]() x,
x,
由PQ=OQ﹣OP可得 ![]() x﹣
x﹣ ![]() x=7,
x=7,
解得:x=7+7 ![]() ≈18.9(cm),
≈18.9(cm),
答:单摆的长度约为18.9cm
(2)
解:由(1)知,∠AOP=60°、∠BOQ=30°,且OA=OB=7+7 ![]() ,
,
∴∠AOB=90°,
则从点A摆动到点B经过的路径长为 ![]() ≈29.295,
≈29.295,
答:从点A摆动到点B经过的路径长为29.295cm
【解析】(1)作AP⊥OC、BQ⊥OC,由题意得∠AOP=60°、∠BOQ=30°,设OA=OB=x,根据三角函数得OP=OAcos∠AOP= ![]() x、OQ=OBcos∠BOQ=
x、OQ=OBcos∠BOQ= ![]() x,由PQ=OQ﹣OP可得关于x的方程,解之可得;(2)由(1)知∠AOB=90°、OA=OB=7+7
x,由PQ=OQ﹣OP可得关于x的方程,解之可得;(2)由(1)知∠AOB=90°、OA=OB=7+7 ![]() ,利用弧长公式求解可得.
,利用弧长公式求解可得.

练习册系列答案
相关题目