题目内容
Ⅰ.先化简 ,再从-2、-1、0、1、
,再从-2、-1、0、1、 中选一个你认为
中选一个你认为 适合的数作为x的值代入求值.
适合的数作为x的值代入求值.
Ⅱ.已知l1:直线y=-x+3和l2:直线y=2x,l1与x轴交点为A.求:
(1)l1与l2的交点坐标.
(2)经过点A且平行于l2的直线的解析式.
解:Ⅰ.原式=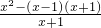 •
•
= •
•
= ,
,
当x=-2时,原式= .
.
Ⅱ.(1)设l1与l2的交点为M,则
由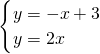 解得
解得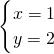 ,
,
∴M (1,2);
(2)设经过点A且且平行于l2的直线的解析式为y=2x+b.
∵l1与x轴交点为A (3,0),
∴6+b=0,
∴b=-6.
则:所求直线的解析式为y=2x-6.
分析:Ⅰ.先通分,然后约分化简,再取值代入即可;
Ⅱ.(1)联立直线y=-x+3和直线y=2x,然后解方程组即可;
(2)可设经过点A且且平行于l2的直线的解析式为y=2x+b,用待定系数法即可得出答案.
点评:本题考查了两条直线相交或平行问题,属于基础题,关键是注意细心运算.
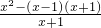 •
•
=
 •
•
=
 ,
,当x=-2时,原式=
 .
.Ⅱ.(1)设l1与l2的交点为M,则
由
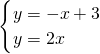 解得
解得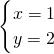 ,
,∴M (1,2);
(2)设经过点A且且平行于l2的直线的解析式为y=2x+b.
∵l1与x轴交点为A (3,0),
∴6+b=0,
∴b=-6.
则:所求直线的解析式为y=2x-6.
分析:Ⅰ.先通分,然后约分化简,再取值代入即可;
Ⅱ.(1)联立直线y=-x+3和直线y=2x,然后解方程组即可;
(2)可设经过点A且且平行于l2的直线的解析式为y=2x+b,用待定系数法即可得出答案.
点评:本题考查了两条直线相交或平行问题,属于基础题,关键是注意细心运算.

练习册系列答案
相关题目
 ,再从0,
,再从0, , 2,1中选择一
, 2,1中选择一 ,再从-2 , 2,
,再从-2 , 2, 中选择一个合适的数代入求值.
中选择一个合适的数代入求值.