题目内容
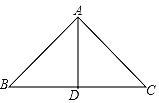
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。
(1)求证:BC是⊙O切线;
(2)若BD=5,DC=3,求AC的长。
【答案】
(1)证明:连接OD;

∵AD是∠BAC的平分线,
∴∠1=∠3.
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴OD∥AC.
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.
(2)蛸:过点D作DE⊥AB,

∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得:BE= ![]() =4,
=4,
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.
∴ ![]() .
.
∴ ![]() .
.
∴AC=6.
【解析】(1)要证BC是⊙O切线.添加辅助线连接OD,证明OD⊥BC。先根据角平分线的定义及等腰三角形的性质,证出OD∥AC(或∠2+∠ADC=90°),再利用平行线的性质得出OD⊥BC,即可证得结论。
(2)过点D作DE⊥AB,根据角平分线上的点到角两边的距离相等,得出CD=DE=3,再利用勾股定理求出BE的长,再根据两组角对应相等的两三角形相似,得出△BDE∽△BAC。得出对应边成比例,建立方程,求解即可;或证明AE=AC,在Rt△ABC中,利用勾股定理求出AC即可。

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目