题目内容
(12分)已知一元二次方程 有两个不相等的实数根。
有两个不相等的实数根。(1)求
 的取值范围;
的取值范围; (2)如果
 是符合条件的最大整数,且一元二次方程
是符合条件的最大整数,且一元二次方程 与
与 有一个相同的根,求此时
有一个相同的根,求此时 的值。
的值。
(1)k<4(2)m=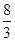 或0解析:
或0解析:
解:(1)∵一元二次方程x2-4x+k=0有两个不相等的实数根,
∴△=(-4)2-4k>0,
∴k<4;
(2)∵k<4,
∴k的最大整数值是3,
∴一元二次方程x2-4x+k=0可化为x2-4x+3=0,
∴x1=3,x2=1,
∵一元二次方程x2-4x+k=0和x2+mx-1=0有一个相同的根,
∴当相同的实数根是3时,
32+3m-1=0,解得m=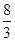 ;
;
当相同的实数根是1时,
12+m-1=0,解得m=0.
故m=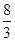 或0;
或0;
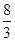 或0解析:
或0解析:解:(1)∵一元二次方程x2-4x+k=0有两个不相等的实数根,
∴△=(-4)2-4k>0,
∴k<4;
(2)∵k<4,
∴k的最大整数值是3,
∴一元二次方程x2-4x+k=0可化为x2-4x+3=0,
∴x1=3,x2=1,
∵一元二次方程x2-4x+k=0和x2+mx-1=0有一个相同的根,
∴当相同的实数根是3时,
32+3m-1=0,解得m=
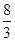 ;
;当相同的实数根是1时,
12+m-1=0,解得m=0.
故m=
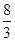 或0;
或0; 
练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目

 有两个不相等的实数根.
有两个不相等的实数根. 的取值范围;
的取值范围; 2
2 ,且一元二次方程
,且一元二次方程 有一个相同的根,求此时
有一个相同的根,求此时 的值.
的值. 有两个实数根.
有两个实数根. 的取值范围;
的取值范围; 有一个相同的根,求此时
有一个相同的根,求此时 的值.
的值. 有两个不相等的实数根.
有两个不相等的实数根.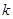 的取值范围;
的取值范围;  有一个相同的根,求此时
有一个相同的根,求此时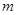 的值.
的值.