题目内容
已知点P在线段4B上,点O在线段AB的延长线上,以点O为圆心,OP为半径作圆,点C是圆O上一点.
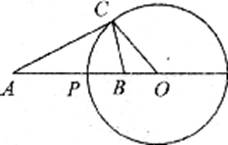
(1)如果AP=2PB,PB=BO.求证△CAO∽△BCO;
(2)如果AP=m(m是常数,且m>1),BP=1,OP是OA、OB的比例中项,当点C在圆周上运动时,求AC:BC的值(结果用含m的式子表示);
(3)在(2)的条件下,讨论以BC为半径的圆B和以CA为半径的圆C的位置关系,并写出相应的m的取值范围.
(1)证明:∵AP=2PB,PB=BO,∴AP=PO.
∴AO=2PO,![]()
∵![]() ∴
∴![]()
∵∠COA=∠BOC,∴△CAO∽△BCO
(2)解:设OP=x,则![]() ,
,![]() .
.
∵OP是OA和OB的比例中项,
∴![]()
解得![]() .即
.即![]()
∴![]() .
.
∵OP是OA和OB的比例中项.即![]()
∵OP=OC,∴![]()
设圆O与线段AB的延长线相交于点Q,当点C、点P、点Q不重合时,
∵∠AOC=∠COB,∴△CAO∽△BCO.∴![]()
∴![]()
![]() 当点C与点P或点Q重合时,可得
当点C与点P或点Q重合时,可得![]()
∴当点C在圆O上运动时,![]()
(3)解:由(2)得,AC>BC,且![]() ,
,
![]() ,圆B和圆C的圆心距d=BC.
,圆B和圆C的圆心距d=BC.
显然,![]() ,∴圆B和圆C的位置关系只能是相交、内切或内含.
,∴圆B和圆C的位置关系只能是相交、内切或内含.
当圆B与圆C相交时,![]() ,得
,得![]() .
.
∵![]() ,∴
,∴![]()
当圆B与圆C内切时,![]() .得m=2.
.得m=2.
当圆口与圆C内含时,![]() .得m>2.
.得m>2.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目