题目内容
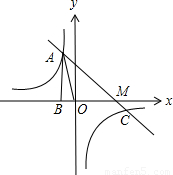
(2009•金平区模拟)已知反比例函数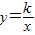 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.(1)求k和m的值;
(2)若直线y=ax+b经过点A,并且经过反比例函的图象上另一点C(n,-
 )
)①求直线y=ax+b解析式;
②设直线y=ax+b与x轴交于M,求△AOC的面积.
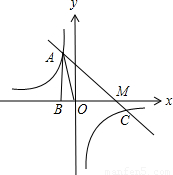
【答案】分析:(1)根据三角形的面积公式,结合点的坐标,求得m的值,再进一步求得k的值;
(2)①首先根据反比例函数的解析式求得n的值,再根据题意,得到关于a,b的方程组,进行求解;
②根据直线的解析式求得点M的坐标,再根据三角形的面积被x轴分割成的两部分面积进行求解.
解答:解:
(1)依题意,得
S△AOB= OB•AB=3,OB=2,
OB•AB=3,OB=2,
∴AB=3,
∴m=3.
即A(-2,3).
把它代入,得
k=-2×3=-6.
(2)①∵双曲线的解析式为y=- ,
,
把(n,- )代入,得
)代入,得
n=- =4.
=4.
∴C(4,- ).
).
∵经过A、C的直线为y=ax+b,则
有 ,
,
解得 ,
,
∴所求直线的解析式y=- x+
x+ ;
;
②在y=- x+
x+ 中,当y=0时,x=2,
中,当y=0时,x=2,
∴OM=2,
∴S△AOM= ×2×3=3,S△COM=
×2×3=3,S△COM= ×2×
×2× =
= ,
,
∴S△AOC=S△AOM+S△COM=3+ =
= ,
,
∴△AOC的面积是 个面积单位.
个面积单位.
点评:能够熟练运用待定系数法求得函数的解析式,能够利用坐标轴把不规则图形的面积转化为规则图形的面积.
(2)①首先根据反比例函数的解析式求得n的值,再根据题意,得到关于a,b的方程组,进行求解;
②根据直线的解析式求得点M的坐标,再根据三角形的面积被x轴分割成的两部分面积进行求解.
解答:解:
(1)依题意,得
S△AOB=
 OB•AB=3,OB=2,
OB•AB=3,OB=2,∴AB=3,
∴m=3.
即A(-2,3).
把它代入,得
k=-2×3=-6.
(2)①∵双曲线的解析式为y=-
 ,
,把(n,-
 )代入,得
)代入,得n=-
 =4.
=4.∴C(4,-
 ).
).∵经过A、C的直线为y=ax+b,则
有
 ,
,解得
 ,
,∴所求直线的解析式y=-
 x+
x+ ;
;②在y=-
 x+
x+ 中,当y=0时,x=2,
中,当y=0时,x=2,∴OM=2,
∴S△AOM=
 ×2×3=3,S△COM=
×2×3=3,S△COM= ×2×
×2× =
= ,
,∴S△AOC=S△AOM+S△COM=3+
 =
= ,
,∴△AOC的面积是
 个面积单位.
个面积单位.点评:能够熟练运用待定系数法求得函数的解析式,能够利用坐标轴把不规则图形的面积转化为规则图形的面积.

练习册系列答案
相关题目
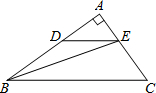 (2009•金平区模拟)如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.
(2009•金平区模拟)如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.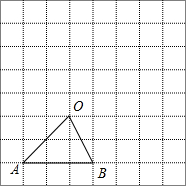 (2009•金平区模拟)如图,在8×8的正方形网格中,△AOB的顶点都在格点上.请在网格中画出△OAB的一个位似图形,使两个图形以点O为位似中心,且所画图形与△OAB的位似为2:1.
(2009•金平区模拟)如图,在8×8的正方形网格中,△AOB的顶点都在格点上.请在网格中画出△OAB的一个位似图形,使两个图形以点O为位似中心,且所画图形与△OAB的位似为2:1.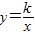 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)