题目内容
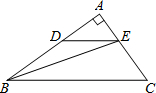 (2009•金平区模拟)如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.
(2009•金平区模拟)如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.(1)求出y关于x的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,△BDE的面积S有最大值,最大值为多少?
分析:(1)根据已知条件DE∥BC可以判定△ADE∽△ABC;然后利用相似三角形的对应边成比例求得
=
;最后用x、y表示该比例式中的线段的长度;
(2)根据∠A=90°得出S△BDE=
•BD•AE,再运用函数性质求解即可.
| AD |
| AB |
| AE |
| AC |
(2)根据∠A=90°得出S△BDE=
| 1 |
| 2 |
解答:解:(1)由题可知,BD=2x,AD=8-2x,
∵DE∥BC
∴△ADE∽△ABC
∴
=
∴
=
∴y=-
x+6,
其中0<x≤4;
(2)∵∠A=90°
∴AE是△BDE中BD边上的高,
∴S△BDE=
BD•AE
∴S=
×2x×(-
x+6)
=-
(x2-4x+4)+6
=-
(x-2)2+6.
∴当x=2时,S有最大值,且最大值为6.
∵DE∥BC
∴△ADE∽△ABC
∴
| AD |
| AB |
| AE |
| AC |
∴
| 8-2x |
| 8 |
| y |
| 6 |
∴y=-
| 3 |
| 2 |
其中0<x≤4;
(2)∵∠A=90°
∴AE是△BDE中BD边上的高,
∴S△BDE=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| 3 |
| 2 |
=-
| 3 |
| 2 |
=-
| 3 |
| 2 |
∴当x=2时,S有最大值,且最大值为6.
点评:本题主要考查相似三角形的判定、三角形的面积及涉及到二次函数的最值问题,找到等量比是解题的关键.

练习册系列答案
相关题目
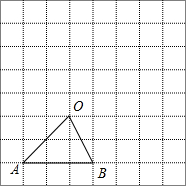 (2009•金平区模拟)如图,在8×8的正方形网格中,△AOB的顶点都在格点上.请在网格中画出△OAB的一个位似图形,使两个图形以点O为位似中心,且所画图形与△OAB的位似为2:1.
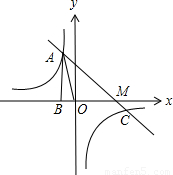
(2009•金平区模拟)如图,在8×8的正方形网格中,△AOB的顶点都在格点上.请在网格中画出△OAB的一个位似图形,使两个图形以点O为位似中心,且所画图形与△OAB的位似为2:1. 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)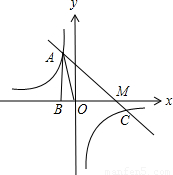
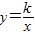 图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3.
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为3. )
)