题目内容
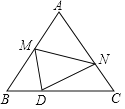
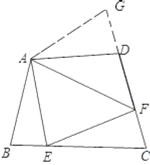
【题目】如图,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,延长FD到点G,使DG=BE,连接AG,下列结论:①△ABE≌△ADG;②△AEF≌△AGF;③EF=BE+DF;④AD+BE>AF,正确的有__________
∠BAD,延长FD到点G,使DG=BE,连接AG,下列结论:①△ABE≌△ADG;②△AEF≌△AGF;③EF=BE+DF;④AD+BE>AF,正确的有__________
【答案】①②③
【解析】
利用SAS即可证出△ABE≌△ADG,从而判断①;根据全等三角形的性质可得AE=AG,∠BAE=∠DAG,从而证出∠EAF=∠GAF,再利用SAS即可证出△AEF≌△AGF,从而判断②;根据全等三角形的性质可得EF=FG,从而判断③;由图可知,无法得出AD+BE>AF,从而判断④.
解:∵∠B+∠ADC=180°,∠ADG+∠ADC=180°
∴∠B=∠ADG
在△ABE和△ADG中,
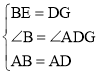 ,
,
∴△ABE≌△ADG(SAS),故①正确;
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD﹣∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△AGF中,
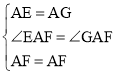 ,
,
∴△AEF≌△AGF(SAS),故②正确;
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF,故③正确;
无法判断AD+BE>AF,故④错误.
综上:正确答案①②③
故答案为:①②③.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目