题目内容
在平面直角坐标系中描出下列各点，A（-4，2）、B（2，4）、C（-1，0），求△ABC的面积．分析：△ABC的面积可转化为“梯形ABFE的面积-△AEC的面积-△BCF的面积”．
解答：解：在平面直角坐标系中描出下列各点如图；
解：S△ABC=S梯形ABFE-S△AEC-S△BCF，
=
×（2+4）×（4+2）-
×3×2-
×3×4，
=18-3-6，
=9．
所以△ABC的面积为9．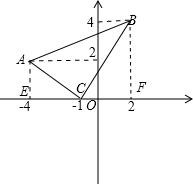
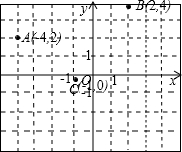
解：S△ABC=S梯形ABFE-S△AEC-S△BCF，
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=18-3-6，
=9．
所以△ABC的面积为9．
点评：此题考查了坐标与图形的性质，将三角形补成四边形，再割成梯形和三角形是解题的关键，此法被称为“割补法”．
练习册系列答案
相关题目
当路况良好时，在干燥的路面上，汽车的刹车距离s与车速v之间的关系如下表所示：
（1）在平面直角坐标系中描出每对（v，s）所对应的点，并用光滑的曲线顺次连接各点；
（2）利用图象验证刹车距离s（m）与车速v（km/h）是否有如下关系：s=
v2+
v0；
（3）求当s=9m时的车速v．
| v/（km/h） | 40 | 60 | 80 | 100 | 120 |
| s/m | 2 | 4.2 | 7.2 | 11 | 15.6 |
（2）利用图象验证刹车距离s（m）与车速v（km/h）是否有如下关系：s=
| 1 |
| 1000 |
| 1 |
| 100 |
（3）求当s=9m时的车速v．
如图，在平面直角坐标系中描出4个点A（0，2），B（-1，0），C（1，-1），D（3，1）
某中学气象兴趣小组为了解某个山区气温随海拔高度的变化情况，现在在不同的海拔高度对气温进行了测量，记录数据如下：
①把上表中y=-
x+23的各组对应值作为点的坐标，在平面直角坐标系中描出相应的点，连接各点并观察所得的图形，猜测与x之间的函数关系，并求出函数关系式；
②已知某种杜鹃花适宜生长在平均气温为17～20℃的山区，估计适宜种植这种杜鹃花的山坡高度的范围．
| 海拔高度x（m） | 500 | 1500 | 2000 | 2500 |
| 气温y（℃） | 20 | 14 | 11 | 8 |
| 3 |
| 50 |
②已知某种杜鹃花适宜生长在平均气温为17～20℃的山区，估计适宜种植这种杜鹃花的山坡高度的范围．
构成一个四边形ABCD．
已知：A（-1，-2），B（3，2），C（0，4）