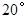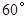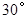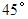题目内容
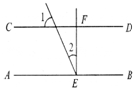
已知:直线AB与直线CD相交于点O,∠BOC= ,
,
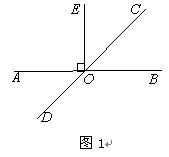
(1)如图1,若EO⊥AB,求∠DOE的度数;
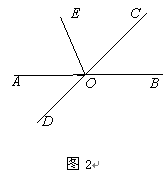
(2)如图2,若EO平分∠AOC,求∠DOE的度数.
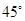 ,
,

(1)如图1,若EO⊥AB,求∠DOE的度数;
(2)如图2,若EO平分∠AOC,求∠DOE的度数.
(1)135°(2)112.5°
解:(1)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=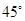 , ………………………………………(1分)
, ………………………………………(1分)
∵EO⊥AB
∴∠AOE=90°,…………………………………………………(2分)
∴∠DOE=∠AOD+∠AOE =135°, …………………………(3分)
(2)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=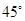 ,∠AOC=135°,
,∠AOC=135°,
∵EO平分∠AOC,
∴∠AOE= ∠AOC =67.5°,…………………………………(4分)
∠AOC =67.5°,…………………………………(4分)
∴∠DOE=∠AOD+∠AOE =112.5°
(1)根据对顶角相等求∠AOD,由垂直的性质求∠AOE,根据∠DOE=∠AOD+∠AOE求解;
(2)由邻补角的性质求∠AOC,根据EO平分∠AOC求∠AOE,再由∠DOE=∠AOD+∠AOE求解.
∴∠AOD=∠BOC=
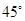 , ………………………………………(1分)
, ………………………………………(1分)∵EO⊥AB
∴∠AOE=90°,…………………………………………………(2分)
∴∠DOE=∠AOD+∠AOE =135°, …………………………(3分)
(2)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=
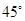 ,∠AOC=135°,
,∠AOC=135°, ∵EO平分∠AOC,
∴∠AOE=
 ∠AOC =67.5°,…………………………………(4分)
∠AOC =67.5°,…………………………………(4分)∴∠DOE=∠AOD+∠AOE =112.5°
(1)根据对顶角相等求∠AOD,由垂直的性质求∠AOE,根据∠DOE=∠AOD+∠AOE求解;
(2)由邻补角的性质求∠AOC,根据EO平分∠AOC求∠AOE,再由∠DOE=∠AOD+∠AOE求解.

练习册系列答案
相关题目
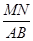 的值.
的值.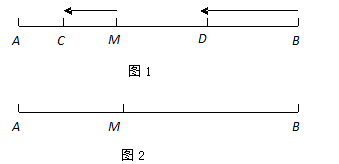

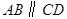 ,
,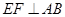 于
于 交
交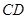 于
于 ,已知
,已知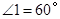 ,则
,则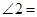 ( ).
( ).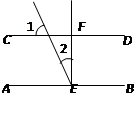
 ,
,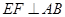 于
于 ,
, 交
交 于
于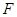 ,已知
,已知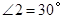 ,则
,则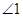 是【 】
是【 】