题目内容
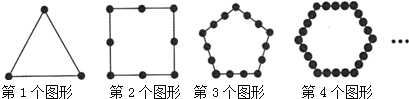
【题目】古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.观察下面的点阵图和相应的等式,探究其中的规律:
(1)下图反映了任何一个三角形数是如何得到的,认真观察,并在④后面的横线上写出相应的等式;
![]()
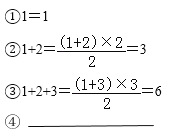
(2)通过猜想,写出(1)中与第八个点阵相对应的等式 ;
(3)从下图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.结合(1)观察下列点阵图,并在⑤看面的横线上写出相应的等式.


(4)通过猜想,写出(3)中与第n个点阵相对应的等式 ;
(5)判断256是不是正方形数,如果不是,说明理由;如果是,256可以看作哪两个相邻的“三角形数”之和?
【答案】(1)1+2+3+4=![]() =10;(2)1+2+3+…+8=
=10;(2)1+2+3+…+8=![]() ;(3)10+15=52;(4)
;(3)10+15=52;(4)![]() =n2;(5)是正方形数,可以看作是120、136两个相邻的三角形数的和.
=n2;(5)是正方形数,可以看作是120、136两个相邻的三角形数的和.
【解析】
(1)根据计算方法写出即可;
(2)根据求解规律,用点阵的序数乘比序数大1的数,再除以2即可;
(3)根据(1)中三角形数的规律写出即可;
(4)用第(n1)个三角形数加上第n个三角形数,整理即可得解;
(5)根据256=162可得是正方形数,然后再计算三角形数即可.
解:(1)④1+2+3+4=![]() =10;
=10;
(2)第八个点阵相应的等式:1+2+3+…+8=![]() ;
;
(3)⑤10+15=52;
(4)第n个点阵相对应的等式:![]() =n2;
=n2;
(5)∵256=162,
∴256是正方形数,
而1+2+3+…+16=136,1+2+3+…+15=120,
∴可以看作是120、136这两个相邻的三角形数的和.

练习册系列答案
相关题目