题目内容
【题目】如图,在平面直角坐标系第一象限中,已知点A坐标为(1,0),点D坐标为(1,3),点G坐标为(1,1),动点E从点G出发,以每秒1个单位长度的速度匀速向点D方向运动,与此同时,x轴上动点B从点A出发,以相同的速度向右运动,两动点运动时间为t(0<t<2),以AD、AB分别为边作矩形ABCD,过点E作双曲线交线段BC于点F,作CD中点M,连接BE、EF、EM、FM.
(1)当t=1时,求点F的坐标.
(2)若BE平分∠AEF,则t的值为多少?
(3)若∠EMF为直角,则t的值为多少?

【答案】(1)点F(2,1);(2)t=![]() ;(3)t=4
;(3)t=4![]() ﹣4
﹣4
【解析】
(1)t=1时,可以求出E点坐标(1,2),并算出经过它的双曲线解析式![]() ,F点和B点的横坐标相同,把B点横坐标x=2代入就可算出F点坐标.
,F点和B点的横坐标相同,把B点横坐标x=2代入就可算出F点坐标.
(2)因为AE![]() BC,所以
BC,所以![]() ,又因为EB平分
,又因为EB平分![]() ,所以
,所以![]() , EF=BF, 在通过坐标用含t的代数式表示EF和BF的长,建立等量关系就可以算出t的值.
, EF=BF, 在通过坐标用含t的代数式表示EF和BF的长,建立等量关系就可以算出t的值.
(3)通过坐标用含t的代数式分别表示出EM,MF,EF的长,因为![]() 是直角,所以
是直角,所以![]() 是直角三角形,运用勾股定理
是直角三角形,运用勾股定理![]() 建立等量关系,算出t即可.
建立等量关系,算出t即可.
(1)t=1时,E点坐标为(1,2),F点横坐标x=2,
设经过E的双曲线为![]() ,
,
把E点坐标代入得:![]() ,
,
再把F点横坐标x=2代入![]() ,
,
得y=1,所以F点坐标为(2,1).
(2)因为A点坐标为(1,0),G点坐标为(1,1),
则t秒后,E点坐标可以表示为(1,1+t),
B点坐标可以表示为(1+t,0),
设经过E点双曲线为:![]() ,
,
把E点坐标代入得:![]() ,
,
F点也在双曲线上,F点横坐标和B相同,
把x=1+t代入函数![]() 得,
得,
y=1,所以F点坐标为(1+t,1),
因为AE![]() BC,所以
BC,所以![]() ,
,
又EB平分![]() ,所以
,所以![]() , EF=BF,
, EF=BF,
即![]() ,
,
解得t=![]() .
.
(3)因为D点坐标为(1,3),M为DC中点,则M点坐标为(1,![]() ),
),
又![]() 是直角,所以
是直角,所以![]() 是直角三角形,
是直角三角形,
由勾股定理![]() ,
,
得:![]() ,
,
解得t=![]() .
.

【题目】苏州太湖养殖场计划养殖蟹和贝类产品,这两个品种的种苗的总投放量只有50吨,根据经验测算,这两个品种的种苗每投放一吨的先期投资,养殖期间的投资以及产值如下表(单位:万元/吨)
品种 | 先期投资 | 养殖期间投资 | 产值 |
贝类产品 | 0.9 | 0.3 | 0.33 |
蟹产品 | 0.4 | 1 | 2 |
养殖场受经济条件的影响,先期投资不超过36万元,养殖期间的投资不超过29万元,设贝类的种苗投放量为x吨,
(1)求x的取值范围;
(2)设这两个品种产出后的总产值为y(万元),试写出y与x之间的函数关系式,并求出当x等于多少时,y有最大值?最大值是多少?
【题目】某中学为促进课堂教学,提高教学质量,对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查.根据收回的问卷,学校绘制了如下图表,请你根据图表中提供的信息,解答下列问题.
编号 | 教学方式 | 最喜欢的频数 | 频率 |
1 | 教师讲,学生听 | 20 | 0.10 |
2 | 教师提出问题,学生探索思考 | ||
3 | 学生自行阅读教材,独立思考 | 30 | |
4 | 分组讨论,解决问题 | 0.25 |
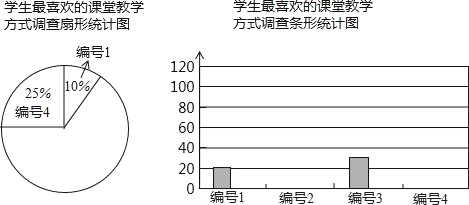
(1)收回的问卷份数为 ,把条形统计图补充完整;
(2)扇形统计图中编号1与编号4的圆心角分别是多少度?
(3)你最喜欢以上哪一种教学方式,请提出你的建议,并简要说明理由.


