��Ŀ����
����Ŀ�����Ķ����в��ϣ�Ȼ�������⣮
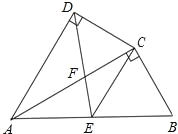
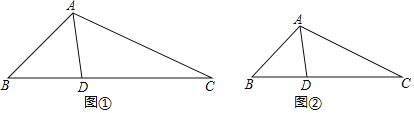
���ϣ��������Σ����ǵ��������Σ�һ����������һ��������Ա��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ������磺��ͼ����AD�ѡ�ABC�ֳɡ�ABD���ADC������ABD�ǵ��������Σ��ҡ�ADC�ס�BAC����ôAD���ǡ�ABC�������ָ��ߣ�
����������⣺
��1����ͼ�����ڡ�ABC�У���B��40�㣬AD�ǡ�ABC�������ָ��ߣ��ҡ�ABD����ADΪ�ױߵĵ��������Σ����CAD���� ���ȣ�
��2���ڡ�ABC�У���B��42�㣬AD�ǡ�ABC�������ָ��ߣ��ҡ�ABD�ǵ��������Σ����BAC�Ķ�����
���𰸡���1��40����2����BAC�Ķ���Ϊ84���111��
��������
��1�����������ε������ָ��߶������⣻
��2��������������ۣ��������ε������ָ��߶���͵��������ε����ʿ���⣮
�⣺��1����AD�ǡ�ABC�������ָ��ߣ�
���DAC�ס�ABC
���CAD����B��40��
�ʴ�Ϊ��40
��2����BD��AD��
��AD�ǡ�ABC�������ָ��ߣ�
���DAC�ס�ABC
���CAD����B��42��
��AD��BD��
���ABD����BAD��42��
���BAC����BAD+��CAD��84��
��AB��BD��
���BAD��69������BDA
�ߡ�AD�ǡ�ABC�������ָ��ߣ�
���DAC�ס�ABC
���CAD����B��42��
���BAC����BAD+��CAD��42��+69����111��
��AB��AD��
���B����ADB��42��
��AD�ǡ�ABC�������ָ��ߣ�
���DAC�ס�ABC
���CAD����B��42��
�ߡ�ADB����DAC+��C��42��+��C��42��
�����AB��AD��
������������BAC�Ķ���Ϊ84����111��

 ��У����ϵ�д�
��У����ϵ�д�