题目内容
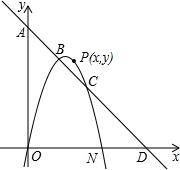 (2013•濠江区模拟)如图所示,抛物线y=ax2+bx+c经过原点O,与x轴交于另一点N,直线y=kx+b1与两坐标轴分别交于A、D两点,与抛物线交于B(1,3)、C(2,2)两点.
(2013•濠江区模拟)如图所示,抛物线y=ax2+bx+c经过原点O,与x轴交于另一点N,直线y=kx+b1与两坐标轴分别交于A、D两点,与抛物线交于B(1,3)、C(2,2)两点.(1)求直线与抛物线的解析式;
(2)若抛物线在x轴上方的部分有一动点P(x,y),求△PON的面积最大值;
(3)若动点P保持(2)中的运动路线,问是否存在点P,使得△POA的面积等于△POD面积的
| 1 | 9 |
分析:(1)把点B、C的坐标代入直线表达式解方程组即可得解,把点B、C、O的坐标代入抛物线的解析式,解三元一次方程组求出a、b、c的值,即可得到抛物线的解析式;
(2)先根据抛物线的解析式求出点N的坐标,再根据三角形的面积公式可知,点P为抛物线的顶点时△PON底边ON上的高最大,面积最大,求出点P的纵坐标,代入面积公式即可得解;
(3)先求出点A、D的坐标,再设点P的坐标为(x,-2x2+5x),根据三角形的面积公式列式得到关于x的一元二次方程,然后求出方程的解,再根据点P在x轴的上方进行判断.
(2)先根据抛物线的解析式求出点N的坐标,再根据三角形的面积公式可知,点P为抛物线的顶点时△PON底边ON上的高最大,面积最大,求出点P的纵坐标,代入面积公式即可得解;
(3)先求出点A、D的坐标,再设点P的坐标为(x,-2x2+5x),根据三角形的面积公式列式得到关于x的一元二次方程,然后求出方程的解,再根据点P在x轴的上方进行判断.
解答:解:(1)根据题意得,
,
解得
,
∴直线的解析式是y=-x+4,
根据图象,抛物线经过点B(1,3)、C(2,2)、(0,0),
∴
,
解得
,
∴抛物线的解析式是y=-2x2+5x;
(2)当y=0时,-2x2+5x=0,
解得x1=0,x2=
,
∴点N的坐标是(
,0),
∴点P的纵坐标越大,则△PON的面积越大,
当点P是抛物线的顶点时,△PON的面积最大,
此时
=
=
=
,
S△PON最大=
×
×
=
;
(3)当x=0时,y=4,
当y=0时,-x+4=0,解得x=4,
∴点A、D的坐标是A(0,4),D(4,0),
设点P的坐标是(x,-2x2+5x),则
×4x=
×
×4×(-2x2+5x),
整理得,2x2+4x=0,
解得x1=0,x2=-2,
此时点P不在x轴的上方,不符合题意,
∴不存在点P,使得△POA的面积等于△POD面积的
.
|
解得
|
∴直线的解析式是y=-x+4,
根据图象,抛物线经过点B(1,3)、C(2,2)、(0,0),
∴
|
解得
|
∴抛物线的解析式是y=-2x2+5x;
(2)当y=0时,-2x2+5x=0,
解得x1=0,x2=
| 5 |
| 2 |
∴点N的坐标是(
| 5 |
| 2 |
∴点P的纵坐标越大,则△PON的面积越大,
当点P是抛物线的顶点时,△PON的面积最大,
此时
| 4ac-b2 |
| 4a |
| -52 |
| 4×(-2) |
| -25 |
| -8 |
| 25 |
| 8 |
S△PON最大=
| 1 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
| 125 |
| 32 |
(3)当x=0时,y=4,
当y=0时,-x+4=0,解得x=4,
∴点A、D的坐标是A(0,4),D(4,0),
设点P的坐标是(x,-2x2+5x),则
| 1 |
| 2 |
| 1 |
| 9 |
| 1 |
| 2 |
整理得,2x2+4x=0,
解得x1=0,x2=-2,
此时点P不在x轴的上方,不符合题意,
∴不存在点P,使得△POA的面积等于△POD面积的
| 1 |
| 9 |
点评:本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求直线与函数的解析式,抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目