题目内容
【题目】如图,I是△ABC的内心,AI的延长线和△ABC的外接圆相交于点D,连接BI、BD、DC.下列说法中错误的一项是( ) 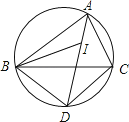
A.线段DB绕点D顺时针旋转一定能与线段DC重合
B.线段DB绕点D顺时针旋转一定能与线段DI重合
C.∠CAD绕点A顺时针旋转一定能与∠DAB重合
D.线段ID绕点I顺时针旋转一定能与线段IB重合
【答案】D
【解析】解:∵I是△ABC的内心,
∴AI平分∠BAC,BI平分∠ABC,
∴∠BAD=∠CAD,故C正确,不符合题意;
∠ABI=∠CBI,∴ ![]() =
= ![]() ,
,
∴BD=CD,故A正确,不符合题意;
∵∠DAC=∠DBC,
∴∠BAD=∠DBC,
∵∠IBD=∠IBC+∠DBC,∠BID=∠ABI+∠BAD,
∴∠BDI=∠DIB,
∴BD=DI,故B正确,不符合题意;
故选D.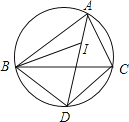
【考点精析】解答此题的关键在于理解三角形的外接圆与外心的相关知识,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心,以及对三角形的内切圆与内心的理解,了解三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.

练习册系列答案
相关题目