��Ŀ����
�Ķ����ϣ���ax2+bx+c=0��a��0��������Ϊx1=
��x2=
����x1+x2=
=-
��x1•x2=
=
�����ϵã���ax2+bx+c=0��a��0��������Ϊx1��x2������x1+x2=-
��x1x2=
�����ô�֪ʶ�������֪x1��x2�Ƿ���x2-x-1=0�����������ⷽ��������ʽ�ӵ�ֵ��
��x12+x22��
�ڣ�x1+1����x2+1����
-b+
| ||
| 2a |
-b-
| ||
| 2a |
| -2b |
| 2a |
| b |
| a |
| b2-(b2-4ac) |
| 4a2 |
| c |
| a |
| b |
| a |
| c |
| a |
��x12+x22��
�ڣ�x1+1����x2+1����
���������ݸ���ϵ���Ĺ�ϵ�õ�x1+x2=1��x1•x2=1��Ȼ�����x12+x22=��x1+x2��2-2x1•x2���ڣ�x1+1����x2+1��=x1•x2+x1+x2+1���ٷֱ���������˼����㼴�ɣ�
����⣺���������x1+x2=1��x1•x2=1��
��x12+x22=��x1+x2��2-2x1•x2=12-2��1=-1��
�ڣ�x1+1����x2+1��=x1•x2+x1+x2+1=1+1+1=3��
��x12+x22=��x1+x2��2-2x1•x2=12-2��1=-1��
�ڣ�x1+1����x2+1��=x1•x2+x1+x2+1=1+1+1=3��
���������⿼����һԪ���η���ax2+bx+c=0��a��0���ĸ���ϵ���Ĺ�ϵ������������Ϊx1��x2����x1+x2=-
��x1•x2=
��
| b |
| a |
| c |
| a |

��ϰ��ϵ�д�
�����Ŀ
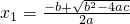 ��
��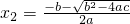 ����
����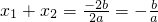 ��
��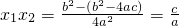 �����ϵã���ax2+bx+c=0��a��0��������Ϊx1��x2������
�����ϵã���ax2+bx+c=0��a��0��������Ϊx1��x2������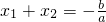 ��
��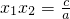 �����ô�֪ʶ�������֪x1��x2�Ƿ���x2-x-1=0�����������ⷽ��������ʽ�ӵ�ֵ��
�����ô�֪ʶ�������֪x1��x2�Ƿ���x2-x-1=0�����������ⷽ��������ʽ�ӵ�ֵ��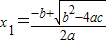 ��
�� ����
����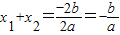 ��
��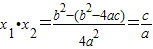 �����ϵã���ax2+bx+c=0��a��0��������Ϊx1��x2������
�����ϵã���ax2+bx+c=0��a��0��������Ϊx1��x2������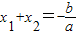 ��
��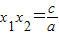 �����ô�֪ʶ�����
�����ô�֪ʶ�����