题目内容
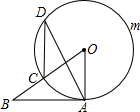 如图,AB切⊙O于点A,BO交⊙O于点C,点D是
如图,AB切⊙O于点A,BO交⊙O于点C,点D是 | CmA |
分析:先根据切线的性质求出∠AOC的度数,再根据三角形内角和定理求出∠AOB的度数,由圆周角定理即可解答.
解答:解:∵AB切⊙O于点A,
∴OA⊥AB,
∵∠ABO=32°,
∴∠AOB=90°-32°=58°,
∴∠ADC=
∠AOB=
×58°=29°.
∴OA⊥AB,
∵∠ABO=32°,
∴∠AOB=90°-32°=58°,
∴∠ADC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题比较简单,解答此题的关键是熟知切线的性质、三角形内角和定理及圆周角定理,有一定的综合性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
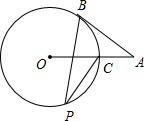 已知:如图,AB切⊙O于点B,OA与⊙O交于点C,点P在⊙O上,若∠BAC=40°,则∠BPC的度数为( )
已知:如图,AB切⊙O于点B,OA与⊙O交于点C,点P在⊙O上,若∠BAC=40°,则∠BPC的度数为( )| A、20° | B、25° | C、30° | D、40° |
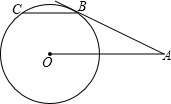 如图,AB切⊙O于点B,OA=2
如图,AB切⊙O于点B,OA=2| 3 |
A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
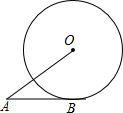 如图,AB切⊙O于点B,AB=4cm,AO=6cm,则⊙O的半径为
如图,AB切⊙O于点B,AB=4cm,AO=6cm,则⊙O的半径为 (2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( )
(2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( ) (2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=
(2012•广东模拟)如图,AB切⊙O于点A,OD⊥弦AC于点D,延长OD,交AB于点B,若∠O=60°,AC=6cm,则AB=