题目内容
已知:2a2+ab-b2=0,求代数式| a |
| b |
| b |
| a |
| a2+b2 |
| ab |
分析:把已知分解因式求出b=2a.b=-a,把原式化简得出原式=-
,分别代入求出即可.
| 2b |
| a |
解答:解:2a2+ab-b2=0,
分解因式得:(2a-b)(a+b)=0,
∴2a-b=0,a+b=0,
∴b=2a.b=-a,
①b=2a时,原式=
,
=
=-
=-4;
②b=-a时,原式=-
=2.
分解因式得:(2a-b)(a+b)=0,
∴2a-b=0,a+b=0,
∴b=2a.b=-a,
①b=2a时,原式=
| a2-b2-(a2+b2) |
| ab |
=
| -2b2 |
| ab |
| 2b |
| a |
②b=-a时,原式=-
| 2b |
| a |
点评:本题主要考查对分式的加减法则,通分,因式分解等知识点的理解和掌握,能求出b=2a和b=-a是解此题的关键.

练习册系列答案
相关题目
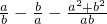 的值.
的值.