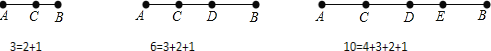题目内容
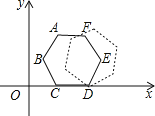
【题目】如图的平面直角坐标系中有一个正六边形ABCDEF，其中C、D的坐标分别为（1，0）和（2，0）．若在无滑动的情况下，将这个六边形沿着x轴向右滚动，则在滚动过程中，这个六边形的顶点A、B、C、D、E、F中，会过点（45，2）的是点 ．
【答案】B
【解析】
试题分析：先连接A′D，过点F′，E′作F′G⊥A′D，E′H⊥A′D，由正六边形的性质得出A′的坐标，再根据每6个单位长度正好等于正六边形滚动一周即可得出结论．
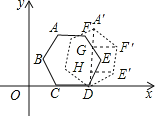
解：如图所示：
当滚动到A′D⊥x轴时，E、F、A的对应点分别是E′、F′、A′，连接A′D，点F′，E′作F′G⊥A′D，E′H⊥A′D，
∵六边形ABCDEF是正六边形，
∴∠A′F′G=30°，
∴A′G=
A′F′=，同理可得HD=，
∴A′D=2，
∵D（2，0）
∴A′（2，2），OD=2，
∵正六边形滚动6个单位长度时正好滚动一周，
∴从点（2，2）开始到点（45，2）正好滚动43个单位长度，
∵
=7…1，
∴恰好滚动7周多一个，
∴会过点（45，2）的是点B．
故答案为：B．
练习册系列答案
相关题目
【题目】为执行中央“节能减排，美化环境，建设美丽新农村”的国策，我市某村计划建造A、B两种型号的沼气池共20个，以解决该村所有农户的燃料问题．两种型号沼气池的占地面积、使用农户数及造价见下表：
型号 | 占地面积 （单位：m2/个 ） | 使用农户数 （单位：户/个） | 造价 （单位：万元/个） |
A | 15 | 18 | 2 |
B | 20 | 30 | 3 |
已知可供建造沼气池的占地面积不超过365m2，该村农户共有492户．
（1）满足条件的方案共有几种？写出解答过程；
（2）通过计算判断，哪种建造方案最省钱？