题目内容
仔细阅读下面的例题，找出其中规律，并解决问题：
例：求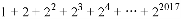
的值.
【解析】
令S＝ ，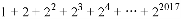
则2S＝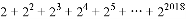
，
所以2S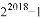﹣S＝
，即S=，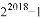
所以＝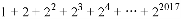
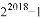
仿照以上推理过程，计算下列式子的值：
①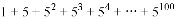 
②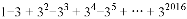 
练习册系列答案
中考解读考点精练系列答案
相关题目
中考解读考点精练系列答案题目内容
仔细阅读下面的例题，找出其中规律，并解决问题：
例：求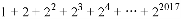的值.
【解析】
令S＝ ，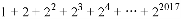
则2S＝ ，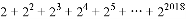
所以2S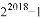﹣S＝ ，即S=，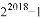
所以＝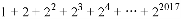
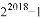
仿照以上推理过程，计算下列式子的值：
① 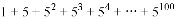②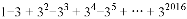
中考解读考点精练系列答案
.
，则该等腰三角形的底角的度数为______．
B. 
C. 
D. 
； 
；
.
