题目内容
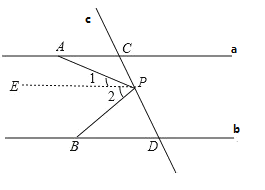
【题目】如图已知直线![]() 直线
直线![]() 和直线
和直线![]() 交于点C和D,在C、D之间有一点P.
交于点C和D,在C、D之间有一点P.
(1)图中∠PAC、∠APB、∠PBD之间有什么关系,并说明理由;
(2)如果P点在C、D之间运动时,∠PAC、∠APB、∠PBD之间的关系是否发生变化?
(3)若点P在直线![]() 上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。
上C、D两点的外侧运动时(点P与点C、D不重合),试探究∠PAC、∠APB、∠PBD之间的关系又是如何?分别画出图形并说明理由。

【答案】(1)∠APB=∠CAP+∠DBP;(2)不发生变化;(3)当P点在DC延长线上时:∠APB=∠DBP-∠CAP;当P点在CD延长线上时:∠APB=∠CAP-∠DBP
【解析】
(1)过点P作EP∥a,根据平行线的性质即可求解;
(2)根据平行线的性质可知不会发生变化;
(3)根据题意作出图形,根据平行线的性质即可求解.
(1)如图,过点P作EP∥a,
∵![]()
∴EP∥a∥b,
∴∠CAP=∠1,∠DBP=∠2,
∵∠APB=∠1+∠2,
∴∠APB=∠CAP+∠DBP
(2)当P点在C、D之间运动时,∠APB=∠CAP+∠DBP,不会发生变化;
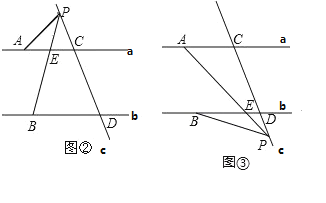
(3)如图②,当P点在DC延长线上时:∠APB=∠DBP-∠CAP.
理由如下:
∵a∥b,∴∠PEC=∠PBD,
∵∠PEC=∠CAP +∠APB
∴∠PBD=∠CAP +∠APB
即∠APB=∠DBP-∠CAP.
如图③当P点在CD延长线上时:∠APB=∠CAP-∠DBP
理由如下:
∵a∥b,∴∠CAP =∠DEP,
∵∠DEP =∠DBP +∠APB
∴∠CAP =∠DBP +∠APB
即∠APB=∠CAP-∠DBP

【题目】为了从甲、乙两人中选拔一人参加射击比赛,现对他们的射击成绩进行了测试,5次打靶命中的环数如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)将下表填写完整:
平均数 | 中位数 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根据以上信息,若你是教练,你会选择谁参加射击比赛,理由是什么?
(3)若乙再射击一次,命中8环,则乙这六次射击成绩的方差会 .(填“变大”或“变小”或“不变”)