题目内容
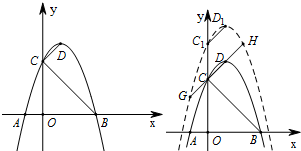
抛物线![]() 的顶点为M,与
的顶点为M,与![]() 轴的交点为A、B(点B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于
轴的交点为A、B(点B在点A的右侧),△ABM的三个内角∠M、∠A、∠B所对的边分别为m、a、b。若关于![]() 的一元二次方程
的一元二次方程![]() 有两个相等的实数根。
有两个相等的实数根。
(1)判断△ABM的形状,并说明理由。
(2)当顶点M的坐标为(-2,-1)时,求抛物线的解析式,并画出该抛物线的大致图形。
(3)若平行于![]() 轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与
轴的直线与抛物线交于C、D两点,以CD为直径的圆恰好与![]() 轴相切,求该圆的圆心坐标。
轴相切,求该圆的圆心坐标。
解:(1)令![]() ,得
,得![]()
由勾股定理的逆定理和抛物线的对称性知△ABM是一个以![]() 、
、![]() 为直角边的等腰直角三角形
为直角边的等腰直角三角形
(2)设![]()
∵△ABM是等腰直角三角形
∴斜边上的中线等于斜边的一半
又顶点M(-2,-1)
∴![]() ,即AB=2
,即AB=2
∴A(-3,0),B(-1,0)
将B(-1,0) 代入![]() 中得
中得![]()
∴抛物线的解析式为![]() ,即
,即![]()
图略
(3)设平行于![]() 轴的直线为
轴的直线为![]()
解方程组
得![]() ,
,![]() (
(![]()
∴线段CD的长为![]()
∵以CD为直径的圆与![]() 轴相切
轴相切
据题意得![]()
∴![]()
解得 ![]()
∴圆心坐标为![]() 和
和![]() 。
。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 某抛物线是由抛物线y=-2x2向左平移2个单位得到.
某抛物线是由抛物线y=-2x2向左平移2个单位得到. 已知抛物线①经过点A(-1,0)、B(4,5)、C(0,-3),其对称轴与直线BC交于点P.
已知抛物线①经过点A(-1,0)、B(4,5)、C(0,-3),其对称轴与直线BC交于点P.