题目内容
【题目】已知抛物线y=x2+bx+c（bc≠0）．
（1）若该抛物线的顶点坐标为（c，b），求其解析式；
（2）点A（m，n），B（m+1，
n），C（m+6，n）在抛物线y=x2+bx+c上，求△ABC的面积；
（3）在（2）的条件下，抛物线y=x2+bx+c的图象与x轴交于D（x1，0），E（x2，0）（x1＜x2）两点，且0＜x1+
x2＜3，求b的取值范围．
【答案】(1) y=x2﹣6x+3；(2)15；(3) ﹣5.5＜b＜﹣1且b≠﹣2．
【解析】（1）根据抛物线的顶点式和顶点坐标（c，b）设解析式，与已知的解析式列等式可求得b和c的值，写出抛物线的解析式；
（2）由A与C的纵坐标相等可得：m和m+6是方程x2+bx+c=n的两根，根据根与系数的关系列方程组可得b和c的值，把B的坐标代入抛物线的解析式中，再把b和c的值代入可得n的值，表示A、B、C三点的坐标，可求△ABC的面积；
（3）先根据（2）求出方程的两根，代入已知0＜x1+
x2＜3中，并将m换成关于b的式子，解不等式可得b的取值范围．
（1）∵抛物线的解析式为：y=x2+bx+c，∴抛物线解析式中二次顶的系数为1，设抛物线的解析式为：y=（x﹣c）2+b，∴（x﹣c）2+b=x2+bx+c，∴
．
∵bc≠0，∴
，∴抛物线的解析式为：y=x2﹣6x+3；
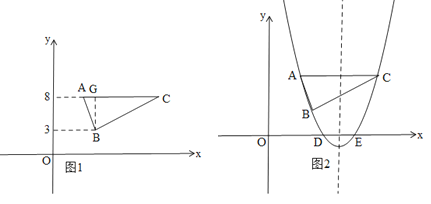
（2）如图1．∵点A（m，n），C（m+6，n）在抛物线y=x2+bx+c上，∴m和m+6是方程x2+bx+c=n的两根，即x2+bx+c﹣n=0，∴
，
解得：
．
∵B（m+1，
n）在抛物线y=x2+bx+c上，∴（m+1）2+b（m+1）+c=n，将b、c代入得：（m+1）2﹣2（m+3）（m+1）+m2+6m+n=n，即n﹣5=n，n=8，∴A（m，8），B（m+1，3），C（m+6，8），∴AC=6．
过B作BG⊥AC于G，则BG=8﹣3=5，∴S△ABC=
×6×5=15；
（3）由题意得：x1+x2=﹣b=2m+6①，x1x2=c=m2+6m+8②．
∵bc≠0，∴b≠0，c≠0，∴m≠﹣2或﹣4．
∵x1＜x2，由①和②得：
．
∵0＜x1+x2＜3，∴0＜3x1+x2＜9，0＜3（m+2）+m+4＜9，0＜4m+10＜9．
∵b=﹣2m﹣6，∴2m=﹣b﹣6．
∵m≠﹣2或﹣4，∴b≠﹣2或2，∴0＜﹣2b﹣12+10＜9，∴﹣5.5＜b＜﹣1且b≠﹣2．
