��Ŀ����
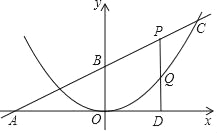
����Ŀ����ͼ��ֱ��y=kx+b�������ύ��A��B���㣬���е�B������Ϊ��0��4����tan��BAO=![]() ��һ�������ߵĶ���Ϊ����ԭ�㣬����ֱ��y=kx+b���ڵ�C��m��8������PΪ�߶�BC��һ���㣨�����B����C�غϣ���PD��x���ڵ�D�����������ڵ�Q.
��һ�������ߵĶ���Ϊ����ԭ�㣬����ֱ��y=kx+b���ڵ�C��m��8������PΪ�߶�BC��һ���㣨�����B����C�غϣ���PD��x���ڵ�D�����������ڵ�Q.
��1����ֱ�ߺ������ߵĺ�����ϵʽ��
��2�����P�ĺ�����Ϊt���߶�PQ�ij���Ϊd�����d��t֮��ĺ�����ϵʽ�������d�����ֵ��
��3���Ƿ���ڵ�P��λ�ã�ʹ���Ե�P��D��BΪ������������ǵ��������Σ�������ڣ�ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x+4��y=
x+4��y=![]() x2����2��d=��
x2����2��d=��![]() t2+
t2+![]() t+4,��t=2ʱ��d�����ֵ
t+4,��t=2ʱ��d�����ֵ![]() ����3�����ڣ�P������Ϊ��2+2
����3�����ڣ�P������Ϊ��2+2![]() ��5+
��5+![]() ����
����![]() ��
��![]() �������ɼ�����
�������ɼ�����
����������1�����������κ��������A�����꣬�����ô���ϵ����������������ߵĽ���ʽ��
��2������P��Q�������ú�t��ʽ�ӱ�ʾ���������������ľ��빫ʽ�������d��t֮��ĺ�����ϵʽ�����ö��㹫ʽ�������d�����ֵ��
��3����PB=BD��PB=PD��BD=PD��������������ۼ���.
�⣺��1����B��0��4����
��OB=4��
��Rt��AOB����tan��BAO=![]() =
=![]() ��
��
��OA=2OB=8��
��A����8��0����
��A����8��0����B��0��4������y=kx+b��![]() �����
����� ��
��
��ֱ��AB�Ľ���ʽΪy=![]() x+4��
x+4��
��y=8ʱ��![]() x+4=8�����x=8����C��8��8����
x+4=8�����x=8����C��8��8����
�������߽���ʽΪy=ax2��
��C��8��8�������64a=8�����a=![]() ��
��
�������ߵĽ���ʽΪy=![]() x2��
x2��
��2����P��t��![]() t+4����0��t��8������Q��t��
t+4����0��t��8������Q��t��![]() t2����
t2����
��d=![]() t+4��
t+4��![]() t2
t2
=��![]() t2+
t2+![]() t+4��
t+4��
��d=��![]() ��t��2��2+
��t��2��2+![]() ��
��
�൱t=2ʱ��d�����ֵ![]() ��
��
��3�����ڣ�
��B��0��4����P��t��![]() t+4����D��t��0����
t+4����D��t��0����
��PB2=t2+��![]() t+4��4��2=
t+4��4��2=![]() t2��DB2=t2+42=t2+16��PD2=��
t2��DB2=t2+42=t2+16��PD2=��![]() t+4��2=
t+4��2=![]() t2+4t+16��
t2+4t+16��
��PB=BDʱ����PBDΪ���������Σ���![]() t2=t2+16�����t1=8����ȥ����t2=��8����ȥ����
t2=t2+16�����t1=8����ȥ����t2=��8����ȥ����
��PB=PDʱ����PBDΪ���������Σ���![]() t2=
t2=![]() t2+4t+16�����t1=2��2
t2+4t+16�����t1=2��2![]() ����ȥ����t2=2+2
����ȥ����t2=2+2![]() ����ʱP������Ϊ��2+2
����ʱP������Ϊ��2+2![]() ��5+
��5+![]() ����
����
��BD=PDʱ����PBDΪ���������Σ���t2+16=![]() t2+4t+16�����t1=0����ȥ����t2=
t2+4t+16�����t1=0����ȥ����t2=![]() ����ʱP������Ϊ��
����ʱP������Ϊ��![]() ��
��![]() ����
����
����������P��������2+2![]() ��5+
��5+![]() ����
����![]() ��
��![]() ����
����

����Ŀ��������һ�����⣺̽������y=-![]() +|x|��ͼ�������ʣ�
+|x|��ͼ�������ʣ�
С������ѧϰ�����ľ��飬�Ժ���y=-![]() +|x|��ͼ�������ʽ�����̽����
+|x|��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y=-![]() +|x|���Ա���x��ȡֵ��Χ�� ��
+|x|���Ա���x��ȡֵ��Χ�� ��
��2������y��x�ļ����Ӧֵ.
x | -2 | -1.9 | -1.5 | -1 | -0.5 | 0 | 1 | 2 | 3 | 4 | �� |
y | 2 | 1.60 | 0.80 | 0 | -0.72 | -1.41 | -0.37 | 0 | 0.76 | 1.55 | �� |
��ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ��

��3���۲�ͼ��������Сֵ�� ��
��4����һ��̽������Ϻ�����ͼ��д���ú�����һ�����ʣ�������Сֵ���⣩�� ��