题目内容
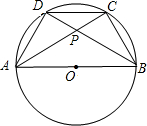如图，已知⊙O中，直径AB=1，弦AC与BD相交于点P，则cos∠BPC的值等于线段
- A.BC的长
- B.AD的长
- C.CD的长
- D.BP的长
C
分析：根据直径所对的圆周角是直角得∠ACB=90°；根据三角函数定义知cos∠BPC=PC：PB；易证△PCD∽△PBA，得PC：PB=CD：AB．
解答：∵AB是直径，
∴∠ACB=90°．
∴cos∠BPC=PC：PB．
∵∠ACD=∠ABD，∠CPD=∠BPA，
∴△PCD∽△PBA．
∴PC：PB=CD：AB=CD：1=CD．
故选C．
点评：此题考查圆周角定理、三角函数定义、相似三角形的判定和性质，难度中等．
分析：根据直径所对的圆周角是直角得∠ACB=90°；根据三角函数定义知cos∠BPC=PC：PB；易证△PCD∽△PBA，得PC：PB=CD：AB．
解答：∵AB是直径，
∴∠ACB=90°．
∴cos∠BPC=PC：PB．
∵∠ACD=∠ABD，∠CPD=∠BPA，
∴△PCD∽△PBA．
∴PC：PB=CD：AB=CD：1=CD．
故选C．
点评：此题考查圆周角定理、三角函数定义、相似三角形的判定和性质，难度中等．
练习册系列答案
相关题目
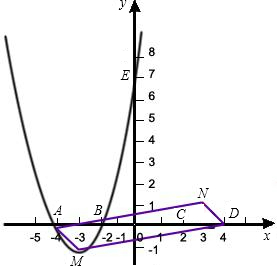如图，已知抛物线C1与坐标轴的交点依次是A（-4，0），B（-2，0），E（0，8）．
10、如图，在铺设铁轨时，两条直轨必须是互相平行的，如图，已知∠1=90°，那么图中的∠5=
学习过三角函数，我们知道在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化．类似的，也可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）．如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时sad A=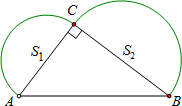
（2012•咸丰县二模）如图，已知在Rt△ABC中，∠ACB=90°，AB=10，分别以AC、BC为直经作半圆，面积分别记为S1、S2，则S1+S2的值等于（ ）