题目内容
抛物线y= x2+2bx与x轴的两个不同交点是O和A,顶点B在直线y=kx上,若△OAB是等边三角形,则b=
x2+2bx与x轴的两个不同交点是O和A,顶点B在直线y=kx上,若△OAB是等边三角形,则b=
- A.±

- B.±3
- C.±

- D.±

A
分析:先根据题意求出O和A的横坐标,然后利用顶点式,依据二次函数的性质即可解答.
解答:已知抛物线y= x2+2bx与x轴的两个不同交点是O和A,令y=0求出x=0或-3b
x2+2bx与x轴的两个不同交点是O和A,令y=0求出x=0或-3b
又由配方法得,原抛物线方程化为y=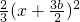 -
-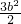
由等边三角形性质得,±3b× =
=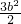 ,
,
解得b=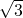 .
.
故选A.
点评:本题涉及二次函数的综合题型,难度中等.
分析:先根据题意求出O和A的横坐标,然后利用顶点式,依据二次函数的性质即可解答.
解答:已知抛物线y=
 x2+2bx与x轴的两个不同交点是O和A,令y=0求出x=0或-3b
x2+2bx与x轴的两个不同交点是O和A,令y=0求出x=0或-3b又由配方法得,原抛物线方程化为y=
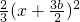 -
-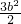
由等边三角形性质得,±3b×
 =
=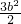 ,
,解得b=
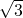 .
.故选A.
点评:本题涉及二次函数的综合题型,难度中等.

练习册系列答案
相关题目